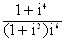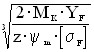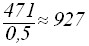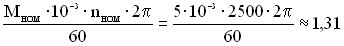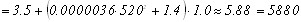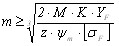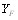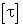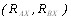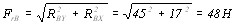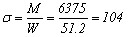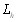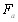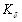Теги - ОСТы Системы стандартов сметные нормы гост

---

Содержание.

Выбор типа электродвигателя для ЭМП……………………4

Кинематический расчет………………………………………7

Расчет валов и разработка их конструкции………………..18

Расчет подшипников………………………………………...21

Расчет фрикционной муфты………………………………..23

Расчет на быстродействие………..…………………………25

Разработка кинематической схемы………………………...26

Список литературы…………………………………………..26

Спецификации.……………………………………………….27

Схема сборки…………………………………………………31

Приложения…………………………………………………..32

Выбор типа электродвигателя для ЭМП.

Поскольку в приводах следящих систем применяются управляемые двигатели, то остановим свой выбор на двигателях серий

ДИД, ДГ, СЛ, ДПР, ДПМ   ([3], с 30-44). Учет напряжения питания и срока службы значительно сужает этот круг. Исключаются двигатели переменного тока ДИД и ДГ и постоянного – СЛ.

КПД двигателей серии ДПМ на 15… 20 % ниже, чем у аналогичных двигателей серии ДПР, а электромеханическая постоянная больше в 2… 2.5 раза, следовательно, останавливаем свой выбор на двигателях серии ДПР.

По сроку службы, условиям эксплуатации и питающему напряжению подходят следующие двигатели:

ДПР-02-H1-01,

ДПР-32-H1-05,

ДПР-32-H1-06,

ДПР-32-H1-07,

ДПР-32-H1-08,

ДПР-42-H1-07,

ДПР-42-H1-08,

ДПР-52-H1-06,

ДПР-52-H1-07,

ДПР-62-H1-06,

ДПР-72-H1-06.

Двигатели серии ДПР – реверсивные, рассчитаны на продолжительный режим работы, могут работать в кратковременном и повторно кратковременном режимах. Предназначены для работы при температуре окружающей среды –60…+70° С, относительной влажности 98% при температуре 40° С и атмосферном давлении от 535 до 3040 ГПа. Допускаются: вибрация мест крепления в любом направлении с частотой от 5 до 2000 Гц при ускорении 10g и амплитуде вибрации не более 1 мм; линейные ускорения до 100g вдоль оси двигателя и до 50g в любом направлении; ударные нагрузки  до 50g в любом направлении. Рабочее положение вала произвольное.

Электромеханическая постоянная времени 0,015…0,02 с. Двигатели могут работать в кратковременном и повторно-кратковременном режимах работы.

Крепление  электродвигателей с обозначением Ф1 осуществляется привертыванием двигателя к корпусу винтами через отверстия во фланце.

Проверим двигатели по необходимой мощности по формуле ([3], с. 13):

       где

io                 – общее передаточное отношение;

ηр                – предполагаемый КПД редуктора;

JH                 – приведенный момент инерции привода;

ωнmax        – максимальная скорость вращения выходного вала;

ωнmax        – максимальное ускорение;

       

               

Для оценочных расчетов будем принимать передаточное отношение всех ступеней приблизительно одинаковыми и равными (3,5…5)

   i1 = i2 = … = in = 3.5 … 5

и КПД первой ступени с учетом подшипников

η1 = η2 = … = ηn ≈ 0.95.

ДПР-2-H1-01.

nном= 9000 об/мин –  номинальная частота вращения вала двигателя;

                         - момент инерции ротора;

                         - общее передаточное отношение;

Согласно известным исследованиям условие минимизации приведенного момента инерции редуктора достигается при оптимальном числе ступеней редуктора   nopt = 3⋅lgi0 ([19], с. 6) и сугубо не равномерном распределении i0 по ступеням – постепенном увеличении передаточных отношений от входа к выходу редуктора.

Такой подход к решению задачи минимизации массы нельзя признать безошибочным по ряду причин. Поэтому примем наиболее простое и часто встречающееся на практике равномерное распределение i0 по ступеням, сохраняя другие допущения при оптимальном распределении.

(3,5…5) – эффективное передаточное отношение для цилиндрических прямозубых зубчатых колес                                                           будем использовать в данном приводе из-за простоты расчета и дешевизны их изготовления);

Для расчета потребляемой мощности выберем количество ступеней n=5

;

ηр = η5 = 0,955 ≈ 0,77

двигатель ДПР –32-H1-01 не подходит , так как не удовлетворяет условию необходимо мощности.

После проведенных расчетов условию необходимой мощности соответствуют следущие типо-размеры двигателей:

Все двигатели имеют некоторый запас по мощности. Однако с точки зрения надежности, предпочительней двигатель ДПР-42-H1-01, .к. у последующих марок двигателей будут увеличиваться габариты и момент на валу, а следовательно и момент инерции ротора, что противоречит требованию задания. Поэтому целесообразно выбрать двигатель ДПР-42-H1-01, его характеристики:

Кинематический расчет.

       Схема 1.

Для быстродействующих приводов приемлемо равномерное распределение общего передаточного отношения по ступеням, определяя его по формуле

.

Принимаем 5 ступеней передач и определяем:

Выбор материалов для конструкции.

Материал выбирают с учетом назначения передачи, характера действующей нагрузки, условий эксплуатации, массы, габаритов и стоимости. Желательно количество материалов, используемых в разрабатываемом приводе, резко ограничить.

Как видно из этих формул

(определение модуля колес [2, ч.1], с 60)

       (определение диаметров колес [9], с 7)

в знаменателе стоят прочностные характеристики материалов. Следовательно, чтобы минимизировать диаметры валов и модуль зубчатых передач, необходимо выбирать материал с высокими по абсолютному значению прочностными характеристиками. В [5], [19] даны рекомендации по выбору материалов. Для зубчатых колес приведены многие материалы, однако я выбрал тот, который, по моему мнению, наиболее подходит моей конструкции: обладает высокой прочностью и дает значительную величину в знаменателе формул для модуля колес Сталь 40Х ГОСТ 4543-71:

σв = 1000 МПа;  ([2, ч.1], с 67)

σ-1 = 400 МПа;

σf = 235 Мпа;

НВ =235–255.

и диаметров валов Сталь 45Х ГОСТ 4543-71:

σв = 1050 МПа;  ([2, ч.1], с 67)

σ-1 = 600 МПа;

σf = 353 Мпа;

НВ =230–280

Для материала плат была Сталь20 [10], которая имеет достаточную прочность  и хорошую обрабатываемость резанием.

Расчет нагрузки на валах.

Полный момент нагрузки на выходном (6-ом) валу МVI складывается из статистического момента нагрузки Мн max и динамического момента МдVI ([2, ч.1], с 67), т.е.

МVI = Мн max+ МдVI,

Приведение моментов от выходных звеньев к двигателю последовательно от передачи к передаче по формуле:

,([4], c 29)где Мi – искомый момент на ведущем звене;  

     Мi+1 – искомый момент на ведомом звене;

     i(i, i+1) – передаточное отношение передачи;

    η – КПД подшипников (0,95…0,99);

МV = 3.13/(0.95⋅3.93) = 0.84 Н⋅м;

МIV = 0.84/(0.95⋅3.93) = 0.225 Н⋅м;

МIII = 0.225/(0.95⋅3.93) = 0.06 Н⋅м;

МII = 0.06/(0.95⋅3.93) = 0.016 Н⋅м;

МI = 0.016/(0.95⋅3.93) = 4.3 Н⋅мм;

Мном= 5.0 Н⋅мм > МI = 4.3 Н⋅мм, что оставляет в силе предварительный выбор двигателя по необходимой мощности.

Оценка диаметров валов передач.

При расчете диаметров валов я учту только кручение, а позже, в проверочных расчетах рассчитаем один из валов на изгиб. Диаметр вала вычисляется по следующей формуле:

, где М – момент на текущем валу;

[τ] – допустимое напряжение кручения.

;

;

;

;

;

.

Определение модуля зубчатых передач передач.

Модуль для открытых цилиндрических прямозубых передач вычисляется по формуле:

    ([2, ч.1], с 60),  где

М – крутящий момент;

YF – коэффициент формы зуба;

K – эмпирический коэффициент 1,1…1,5

z – число зубьев рассчитываемого колеса;

φ bm= 8 – коэффициент ширины зубчатого венца;

[σF] – допустимое напряжение изгиба.

Выбираем количество зубьев шестерни z1 = z3 = z5 = z7 = z9 = 17,      тогда количество зубьев колес равно:

z2 = z4 = z6 = z8 = z10 = i1⋅z1= 3,93⋅17=66,81

из стандартного ряда ([19], с 10) выбираем ближайшее большее значение z2 = 67.

Полагая, что материалы всех колес передачи одинаковы, расчет веду по шестерне, для которой z1 = 17, этому значению числа зубьев соответствует следующее значение коэффициента формы зуба YF = 4,3.

Расчетные значения модулей:

mV, VI >= 0.81 мм;

mIV, V >= 0.52 мм;

mIII, IV >= 0.34 мм;

mII, III >= 0.22 мм;

mI, II >= 0.14 мм;

Округляем полученные значения модулей до ближайших больших из стандартного ряда модулей  ([19], c 15):

mV, VI = 0.8 мм;

mIV, V = 0.6 мм;

mIII, IV = 0.4 мм;

mII, III = 0.25 мм;

mI, II = 0.15 мм.

По конструктивным соображениям увеличиваем mII, III и mI, II до 0.3 мм.

Определение основных размеров зубчатых колес.

Ступень V, VI:

d9 = mV, VI⋅z9 = 0.8⋅17 =  13.6мм;                              ([2, ч.2], с 87])

d10 = mV, VI⋅z10 = 0.8⋅67 =  53.6мм;

b9 = b10 = mV, VI⋅ψbm = 0.8⋅8 =6.4 мм.

Ступень IV, V:

d7 = mIV, V⋅z7 = 0.6⋅17 = 10.2 мм;                             

d8 = mIV, V⋅z8 = 0.6⋅67 = 40.2 мм;

b7 = b8 = mIV, V⋅ψbm = 0.6⋅8 =4.8 мм.

Ступень III, IV:

d5 = mIII, IV⋅z5 = 0.4⋅17 = 6.8 мм;                             

d6 = mIII, IV⋅z6 = 0.4⋅67 = 26.8 мм;

b5 = b6 = mIII, IV⋅ψbm = 0.4⋅8 =3.2 мм.

Ступени  II, III; I,II.

d3 = d1 = mII,III⋅z3 = 0.3⋅17 = 5.1 мм;                             

d4 = d2 =mII,III⋅z4 = 0.3⋅67 = 20.1 мм;

b4 = b3 = b2 = b1 =mII,III⋅ψbm = 0.3⋅8 =2.4 мм.

Значение диаметра шестерни d1 = 2.4 мм получилось меньше, чем значение вала двигателя d = 5.27 мм, на котором она сидит, следовательно, необходимо увеличить количество ступеней.

Из конструкторских соображений приму передаточное отношение зубчатой передачи iI, II= 1 и коэффициент полезного действия ηк = 0,94

( [19], c 3).

Проверим, удовлетворяет ли двигатель ДПР-42-H1-01 новой контрукции. Для расчета  выберем количество ступеней n=6

;

ηр = ηк η5 = 0,94⋅0,955 ≈ 0,727

двигатель ДПР – 42-H1-01 удовлетворяет условию необходимо мощности.

Схема 2.

       

Общее передаточное отношение:

.

Принимаем 6 ступеней передачи и определяем:

iI, II =1

iII, III = iIII, IV = iIV, V = iV, IV = 3.93;

Расчет нагрузки на валах.

МVII = 3.13 Н⋅м;

МVI = 3.13/(0.95⋅3,93) = 840 Н⋅мм;

МV1 = 840/(0.95⋅3,93) = 225 Н⋅мм;

МIV = 225/(0.95⋅3,93) = 60 Н⋅мм;

МIII = 60 /(0.95⋅3,93) = 16 Н⋅мм;

МII = 16/(0.95⋅3,93) = 4.3 Н⋅мм;

МI = 4.3/(0.95⋅3,1) = 4.6 Н⋅мм.

Оценка диаметров валов передач.

, где М – момент на текущем валу;

[τ] – допустимое напряжение кручения.

;

;

;

;

;

;

.

Определение модуля зубчатых передач передач.

   

Выбираем количество зубьев шестерни z1 = z3 = z5 = z7 = z9 = 17,      тогда количество зубьев колес равно:

z2 =17

z4 = z6 = z8 = z10 = i1⋅z1= 3,93⋅17=66,81

из стандартного ряда ([19], с 10) выбираем ближайшее большее значение z2 = 67.

Расчетные значения модулей:

mVI, VII >= 0.809 мм;

mV, VI >= 0.52 мм;

mIV, V >= 0.34 мм;

mIII, IV >= 0.22 мм;

mII, III >= 0.14 мм;

mI, II >= 0.143 мм;

Округляем полученные значения модулей до ближайших больших из стандартного ряда модулей  ([19], c 15):

mVI, VII = 0.8 мм;

mV, VI = 0.6 мм;

mIV, V = 0.4 мм;

mIII, IV = 0.25 мм;

mII, III = 0.15 мм

mI, II = 0.15 мм.

По конструктивным соображениям увеличиваем mII, III , mI, II  и mIII, IV до 0.3 мм.

Определение основных размеров зубчатых колес.

Ступень VI, VII:                               ([2, ч.2], с 87])

d11 = mVI, VII⋅z11 = 0,8⋅ 17 = 13,6 мм;                             

d12 = mVI, VII⋅z12 = 1⋅67 = 53,6 мм;

Ступень V, VI:

d9 = mV, VI⋅z9 = 0.6⋅17 =  10,2 мм;

d10 = mV, VI⋅z10 = 0.6⋅67 =  40,2 мм;

Ступень IV, V:

d7 = mIV, V⋅z7 = 0.4⋅17 = 6,8 мм;                             

d8 = mIV, V⋅z8 = 0.4⋅67 = 26,8 мм;

Ступени III, IV; II, III; I,II:

d5 = d3 = d1 = mIII, IV⋅z5 = 0.3⋅17 = 5.1 мм;                             

d6 = d4 = d2 = mIII, IV⋅z6 = 0.3⋅67 = 20.1 мм;

При такой конструкции вал двигателя и первый вал будут пересекаться, поэтому увеличу передаточное отношение.

Из конструкторских соображений приму передаточное отношение конической передачи передачи  равное двум.

Схема 3.

Общее передаточное отношение:

.

Принимаем 6 ступеней передачи и определяем:

iI, II =2

iII, III = iIII, IV = iIV, V = iV, VI =  iVI, VII = 3.425;

Расчет нагрузки на валах.

МVII = 3.13 Н⋅м;

МVI = 3.13/(0.95⋅3,425) = 962 Н⋅мм;

МV1 = 962/(0.95⋅3,425) = 296 Н⋅мм;

МIV = 296/(0.95⋅3,425) = 91 Н⋅мм;

МIII = 91 /(0.95⋅3,425) = 28 Н⋅мм;

МII = 28/(0.95⋅3,425) = 8.6 Н⋅мм;

МI = 8.6/(0.94⋅2) = 4.6 Н⋅мм.

МI = 4.6 Н⋅мм < 5 Н⋅мм = Мном двигателя ДПР-42-H1-01, что оставляет его выбор в силе.

Оценка диаметров валов передач.

, где М – момент на текущем валу;

[τ] – допустимое напряжение кручения.

;

;

;

;

;

;

.

Определение модуля зубчатых передач передач.

   

Выбираем количество зубьев шестерни z1 = z3 = z5 = z7 = z9 = 17,      тогда количество зубьев колес равно:

z2 =34

z4 = z6 = z8 = z10 = i1⋅z1= 3,425⋅17=58,225

из стандартного ряда ([19], с 10) выбираем ближайшее большее значение z2 = 60.

Расчетные значения модулей:

mVI, VII >= 0.847 мм;

mV, VI >= 0.57 мм;

mIV, V >= 0.38 мм;

mIII, IV >= 0.26 мм;

mII, III >= 0.17 мм;

mI, II >= 0.143 мм;

Округляем полученные значения модулей до ближайших больших из стандартного ряда модулей  ([19], c 15):

mVI, VII = 1 мм;

mV, VI = 0.6 мм;

mIV, V = 0.4 мм;

mIII, IV = 0.3 мм;

mII, III = 0.2 мм;

mI, II = 0.15 мм.

По конструктивным соображениям увеличиваем mII, III и mI, II до 0.3 мм.

Оценим модуль шестерни, которая сажается на вал двигателя по формуле                                        ( из курса ОКМиП  V семестра)

Оказывается, что модуль шестерни должен быть не менее 0,43 мм, т.е равняться 0,5.Тогда принимаю следующие значения модулей:

mVI, VII = 1 мм;

mV, VI = 0.6 мм;

mIV, V = 0.5 мм;

mIII, IV = 0.4 мм;

mII, III = 0.4 мм;

mI, II = 0.5 мм.

Определение основных размеров зубчатых колес.

Ступень VI, VII:                               ([2, ч.2], с 87])

d11 = mVI, VII⋅z11 = 1⋅ 17 = 17 мм;                             

d12 = mVI, VII⋅z12 = 1⋅60 = 60 мм;

Ступень V, VI:

d9 = mV, VI⋅z9 = 0.6⋅17 =  11.4 мм;

d10 = mV, VI⋅z10 = 0.6⋅60 =  37.2 мм;

Ступень IV, V:

d7 = mIV, V⋅z7 = 0.5⋅17 = 9.5 мм;                             

d8 = mIV, V⋅z8 = 0.5⋅60 = 31 мм;

Ступени III, IV; II, III:

d5 = d3 = mIII, IV⋅z5 = 0.4⋅17 = 6.8 мм;                             

d6 = d4 = mIII, IV⋅z6 = 0.4⋅60 = 24.8 мм;

Т.к. фактически значения модулей ступеней передач меньше, а увеличение модуля приводит к увеличению ширины колес,  то необходимо компенсировать это увеличение. Сделать это можно, определив оптимальное значение коэффициента ширины зуба ψbm:

Для ступени III, IV:

ψbm= =2.21,

значения ψbm других ступеней будут меньше, т.к. ψbm= М⋅С,

где  М - момент на соответствующем валу,

        С = - величина постоянная для всех ступеней, а

МIII > МII > МI .

Так, учитывая, что минимальное значение ψbm= 3 ([2, ч. 1], с 61), принимаю ψbm  для ступеней III, IV; II, III; I, II равным 3. Следовательно, толщина колес

  b3 = b4 = b5 = b6 = 0.5⋅3 = 1.5 мм;

Для ступени IV, V:

ψbm= =3.7 ≈ 4

  b7 = b8  = 0.5⋅4= 2 мм

  b9 = b10 = m⋅ψbm V, VI = 0.6⋅8 = 4.8 мм

  b11 = b12 = m⋅ψbm VI, VII = 1⋅8 = 8 мм.

Расчет параметров конической передачи.

Внешний делительный диаметр:

                                  de = mez 

de1 = 0.5*17 = 8.5 мм;

de2 = 0.5*34 = 8.5 мм;

Угол делительного конуса:

δ1 = arctg (z1 / z2 ) = arctg (17 / 34 ) = arctg 0.5 = 26° 34′

δ2 = 90 - δ1 = 90 - 26° 34′ = 63° 26′

Внешнее конусное расстояние:

                                                    Re =

Re =   мм.

Ширина зубчатого венца:

                                                     b≤ 0.3 Re

Принимаем b = 2.5 мм.

Среднее конусное расстояние:

                                                    R = Re – 0.5b

R =9.5 – 0.5*2.5 = 8.25 мм.

Средний окружной модуль:

                                                   

m = 0.5*8.25/9.5 = 0.434 мм.

Средний делительный диаметр:

                                                     d = mz

d1 = 0.434*17 = 7.38 мм;

d2 = 0.434*34 = 14.8 мм;

Расчет валов и разработка их конструкции. 

В соответствии с условиями работы выбираем для вала сталь 45Х ГОСТ 4543 - 71 ([5], с 67) со следующими характеристиками ([9], прил.2, с 32):

HB = 229-280, σв = 1050 МПа, σТ = 850 МПа, τТ = 480 МПа, τ-1 = 230 МПа.

Значение крутящего момента на валу Т = МVI = 3.13 Н⋅м.

Диаметр вала под посадку зубчатого колеса (поскольку вал тихоходный, для условного расчета на кручение выбираем [τ] = 35 МПа):

мм.

Округляем полученное значение до ближайшего большего из стандартного ряда, следовательно d = 8 мм.

Определение расчетных нагрузок и опорных реакций.

Согласно кинематической схеме колесо является ведомым, следовательно

вертикальная плоскость:

       RAY                                                                                        RBX

                                                                                                 

                                    l1                                                      l2                                                                   

                                                           R1

горизонтальная плоскость:

                                                                                                            RBY

                                               l1                                                                  l2

                                        

                                     

RAX                                                                        P1

l1 =  26 мм;

l2 = 20 мм.

P =                                                      R = P⋅tgα     (α = 20°)     ([9], c 21).

P1 = ;                 R1 = 104.3⋅0.364 = 33.9 H;

По полученным значениям расчетных нагрузок определяем опорные реакции в вертикальной и горизонтальной плоскостях.

   RBY (l1 + l2) = R1 l1

RAY = R1 - RBY = 33.9 - 19.16 = 14.74 H,

RAX = RBX - P1 = 58.97 - 104.3 = - 45.36 H

Полученные эпюры:

Вертикальная плоскость:

                               l1                                             C              l2             

                                                    

                                                                    383.2 H мм

Горизонтальная плоскость:

                                 l1                                  C           l2                  

                                            1179.4 H мм       

Из полученных эпюр видно, что наиболее опасными являются сечение С (место посадки колеса). Действующие моменты и напряжения в нем:

Сечение С:

Суммарный изгибающий момент

Крутящий момент на валу

Мк = 3130 Н м

Для диаметра вала d = 8 мм

W = 0.1⋅d3 = 51,2 мм3                                                             ([9], c 22).       

Wp ≈ 0.2⋅d3 = 101,4 мм3.

Напряжение при изгибе    .

Напряжение при кручении .

Номинальное эквивалентное напряжение в опасном сечении

Расчет на статическую прочность.

Запас прочности по пределу текучести:

nТ =

Кп – коэффициент перегрузки.

Условие выполняется для сечения С, следовательно, и для других сечений вала.

Расчет на выносливость.

Проверю необходимость расчета на выносливость для сечения С, где  рядом находятся шпонка и штифт.

Сечение С:

                                            ([9], c 24)

Т.к. диаметр вала d = 8.0, то коэффициент ε не учитывается.

Т.к. в сечении С имеется несколько источников концентрации напряжений , то следует принимать те, которые дают наибольшие значения коэффициентов концентрации напряжений Кσ. Его значения

в месте поперечного отверстия : Кσ = 2.1 ([9],  прилож. 11);

в месте шпоночной канавки при выполнении концевой фрезой: Кσ=2.26

                                                                                            ([9],  прилож. 10).

Выбираю Кσ=2.26. Тогда

Условие выполняется, следовательно, сечение С на выносливость проверять необходимости нет.

Расчет подшипников.

Анализируя устройство будущей конструкции, видим, что наиболее нагруженным в радиальном направлении является выходной вал редуктора. На него действует самый большой крутящий момент, а про осевую нагрузку со стороны выходного вала привода нам ничего не известно ⇒ будем предполагать, что она отсутствует.

Из проектного расчета вала на статическую прочность, который был произведен с учетом крутящего момента, был ориентировочно определен диаметр выходного конца вала. При известном выходном диаметре вала диаметр посадочного места вала под подшипник определяю из конструктивных соображений с учетом технологии изготовления вала и сборки подшипникового узла.

RAX = 45,36 H,                              RBX = 58,97 H, 

RAY = 14,74 H,                              RBY = 19,16 H.

Таким образом, радиальные нагрузки, действующие на подшипники равны:

Оценка диаметра вала и подбор подшипников.

Диаметр вала определяю по формуле:

,  где Мпр = , подставляя это значение в вышеприведенное выражение, получаю:

мм,

таким образом, нужно делать проверку подшипников с внутренним диаметром d = 6 мм, однако по конструктивным соображениям(чтобы в конструкции использовалось минимальное количество типов подшипников) проверим  подшипник с диаметром d = 5 мм

Проверяю подшипник №1000093* по динамической грузоподъемности:

, где

P  – радиальная нагрузка;

n = об/мин – частота вращения;

Lh = 400 ч – продолжительность     работы.

P = VFrKδKT

V – коэффициент вращения,

KT – температурный коэффициент,

Kδ – коэффициент безопасности.

V = 1, т.к. вращается внутреннее кольцо подшипника относительно направления нагрузки

KT = 1 ([8], табл.11),

Kδ = 1,5([8], табл.10), следовательно,

P = KδFrА = 1,5*47,7=71,55H.

Н,

следовательно, в узле А допустимо применять этот тип подшипника.

Такой же подшипник ставлю в узел В и проверяю его грузоподъемность:

P = VFrKδKT

P = KδFrB = 1,5*62=93 H.

Н,

следовательно, в узле В также допустимо применять этот тип подшипника.

Расчет фрикционной муфты.

В настоящее время к ЭМП приборных устройств предъявляются повышенные требования надежности. Для предохранения передачи от перегрузок на выходном валу, которые могут возникать, в частности, при срабатывании механического стопора применена фрикционная предохранительная муфта.

Для уменьшения габаритов пружины полумуфты, а также  специальные вставки на зубчатом колесе выполнены из материала, обладающим повышенным коэффициентом трения (резина) и в то же время удовлетворительной технологичностью.

Фрикционные муфты состоят из двух половин, прижатых одна к другой с определенной силой, величину которой можно регулировать. Когда величина крутящего момента на ведомой оси превышает величину момента сил трения в муфте, одна половина ее начинает скользить по отношению к другой. Прижатие полумуфт к фрикционным обкладкам происходит за счет пружины. Силу прижатия можно регулировать с помощью гайки, навертываемой на резьбу вала. Сила прижатия пружины Р рассчитывается по следующей формуле:

.

Радиус r должен быть меньше радиуса впадин, оценю его:

Диаметр окружности впадин колеса:

df = d - 2( 1 + c*)m = 60 - 2*1.35*1 =57.3 мм.

Однако, по конструкторским соображениям следует принять  r = 15 мм. Тогда

Берем значение эмпирического коэффициента С из интервала 6…12

Вычисляем для выбранного С = 8 коэффициент:

;  kτ=1.17

Диаметр ступицы муфты, на которую будет ложиться пружина, равен 16 мм, значит, Dпр = 18.28 мм и d = 2.28 мм. Возьмем диаметр проволоки пружины из стандартного ряда d = 2.5 мм. Тогда  С = 7,4, kτ=1.19, Dпр = 18.5 мм.

Для уменьшения габаритов в осевом направление пружины и, соответственно, муфты, возьмем небольшое число рабочих витков Iр = 3. Проверю условие прочности:

τ=8PCkτ / π *d2

τ=8*521.67*8*1,19/(3,14*6.25) = 2023 > [τ] = 500 МПа, следовательно,  условие прочности не выполняется.

Выберу другие материалы, например, сталь-резина, для которых коэффициент трения значительно больше f = 0.8.   ([11], c 10)

Тогда

τ=8*130*10*1,19/(3,14*6.25) = 466.67 <[τ]=500 МПа, условие прочности выполняется.

Рассчитаем осевое перемещение одного витка λ (величина деформации) при нагрузке:

λ=8 P D3iраб./G d4=8*130*18,53 3/(8*104*2,54)=6,32 мм.

Рассчитаем длину пружины в свободном состоянии:

Ho=1.3*λ + d⋅(iраб + iконц)=1,3*6,32 + 2,5* (3 + 2)=20,7 мм.

Расчет на быстродействие.

Повышение быстродействия привода достигается минимизацией приведенного момента инерции.

Одним из главных недостатков известного подхода к повышению быстродействия ЭМП является игнорирование момента инерции ротора двигателя Jдв.

Рассчитаем общий приведенный момент инерции Jпр и выясним долю приведенного момента редуктора Jр пр в Jпр, чтобы выяснить, насколько вообще имеет смысл заниматься математической минимизацией Jр пр как части общего момента инерции привода.

Jпр=Jдв + Jр пр  + Jн пр , где

                                              Jдв - момент инерции ротора двигателя;

                                                  Jр пр - приведенный момент инерции              ретуктора;

                                                  Jн пр - приведенный момент инерции нагрузки;

Jдв=1700 г⋅мм2

Jр пр ≈ Jш + , где Jк  - момент инерции колеса;

                                                             Jш - момент инерции шестерни

Моменты инерции колеса и шестерни можно найти по формулам [см. 4] :

Jш=;                  Jк=,

где  dш  и  dк - диаметры делительных окружностей шестерни и колеса,

       в=ψm⋅m - ширина венца,

       ρ=7,85 г /см3=7,85 ⋅ 10-3 (г / мм3)

Jш1=(г / мм2)

Jк2=(г / мм2)

Jш3=(г / мм2)

Jк4=(г / мм2)

Так как Jк >> Jш , то моментом инерции шестерни можно пренебречь, тогда формула будет выглядеть следующим образом:

Jр пр ≈ Jш1 + ≈ (г / мм2)

Jн пр=(г / мм2)

Таким образом общий приведенный момент равен:

Jпр=Jдв + Jр пр  + Jн пр=1700 + 39,7+ 281,4 ≈ 2021 (г / мм2)

Анализируя составляющие данной формулы можно заметить, что

Jр пр  меньше порядком ,чем Jдв. Значит, в данном случае нет смысла заниматься минимизацией приведенного момента редуктора , т.к.  он составляет всего лишь 2%  от общего приведеннго момента.

Расчет редуктора на быстродействие обычно сводиться  к определению электромеханической постоянной редуктора Тэм и определению времени его разгона Траз.

Постоянная времени редуктора определяется в виде

                                           Тэм=,

где  J – приведенный момент инерции ,

      Тэм =25,9 мс

Время разгона редуктора Tраз=3Тэм     ([19], c 35)

Разработка кинематической схемы.

После анализа исходных данных и проведенных расчетов, учитывая требование перпендикулярного расположения входного и выходного валов предложен окончательный вариант кинематической схемы. Взаимное расположение валов меняется на первой ступени конической передачей с передаточным число , равным 2, передаточные числа остальных ступеней равномерно распределены, что допускается заданным критерием проектирования –максимальным быстродействием.

  В редукторе имеется 6 валов, не считая вала двигателя , первые три – это валы – шестерни.

Колеса № 8,9, № 10,11 являются сборными .

Кроме того, на последнем валу для защиты редуктора от перегрузок предусмотрена предохранительная муфта. Для обеспечения и контроля требуемого угла поворота выходного вала  предусмотрены: электрический ограничитель, выполненный на микропереключателях, механический упор, потенциометр. Для обеспечения быстрого и надежного соединения электрических цепей привода с внешними устройствами предусмотрен унифицированный разъем, который крепится к плате № 1 с помощью кронштейна.

Конструкция корпуса редуктора—двухплатная открытая, платы соединяются стойками. Подшипники устанавливаются в платы в стаканах, за исключением одного, который ставиться в крышку–стакан.

Для уменьшения габаритов к плате №2 крепиться стакан выходного вала.

Потенциометр крепится к плате № 1 с помощью кронштейна. В плате №2 предусмотрены четыре  отверстия для монтажа привода следящей системы к внешнему устройству.

Двигатель крепится  к скобе между платами.

Список литературы.

1. Атлас конструкций элементов приборных устройств. Под ред. Тищенко 0.Ф, - М.: Машиностроение, 1982, 116 с.
2. Элементы приборных устройств. Курсовое проектирование. Под ред. Тищенко 0.Ф, - М.: Высшая школа, 1978. - Ч. 1 и Ч.2.
3. Коваленко А.П., Буцев А.А. Выбор исполнительных электродви­гателей приборных устройств. Учебное пособие... М., МВТУ, 1981.
4. Буцев А,А., Коваленко А.П,, Котов А.Н. Проектирование приборных приводов. Учебное пособие... МВТУ, 1988.
5. Матвеев В.И. Элементы приборных устройств. Разработка кон­структорской документации. Учебное пособие. МВТУ, 1977.
6. Тищенко О.Ф., Веселова Е.В., Нарыкова Н.И. Оформление рабочих чертежей деталей и узлов. Метод, указания. МВТУ, 1986.
7. Матвеев В,И„ Капитанова 3.Г., Конструкции зубчатых колес приборов. Учебное пособие. МВТУ, 1980.
8. Матвеев В.И. Элементы приборных устройств. Расчет подшипников качения и проектирование подшипниковых узлов приборов. Учебное пособие. МВТУ, 1978.
9. Веселова Е.В., Нарыкова Н.И. Расчет и конструирование валов и осей приборов, МВТУ, 1980.
10. Кокорев Ю.А. Элементы приборных устройств. Проектирование корпусных деталей приборов. МВТУ, 1980.
11. Велищанский А,В., Климов В.Н., Koтов А.Н. Конструкционные материалы в приборостроении. Уч. пособ., МВТУ, 1987.
12. Веселова Е.В., Нарыкова Н.И,, Ожерельев А.Я. Вспомогательные материалы в конструкциях приборов. Уч. пособ. МВТУ, 1986.
13. Торгов А.М. Общие требования к расчетно-пояснительной записке проекта по курсу "Элементы приборных устройств". МВТУ, 1987.
14. Киселев Л.Т. Соединения в приборостроении. Часть 1, 1974; Часть 2, 1976. МВТУ.
15. Баранов В.Н,, Капитанова З.Г. Расчет и конструирование потен- циометров приборов. Учебное пособ., МВТУ, 1982. 
16. Справочник конструктора точного приборостроения . Под ред. Явленского К.Н.... Л. Машиностроение, 1989.
17. Чурабо Д.Д. Детали и узлы приборов. Конструирование и расчет. Справочное пособие. М., Машиностроение, 1975.
18. Кокорев Ю.А. Способы расчета точностных характеристик дета-  лей и узлов приборов. МГТУ, 1992. 
19. Матвеев В.И. Расчет зубчатых передач редукторов следящих систем. Учебное пособие. МГТУ, 1986. 

> Категория: строительные конструкции дома из бруса Отраслевые стандарты строительные правила сруб дома

Поделитесь этой записью или добавьте в закладки