Теги - гост р ГЭСН Законы ОСТы

---

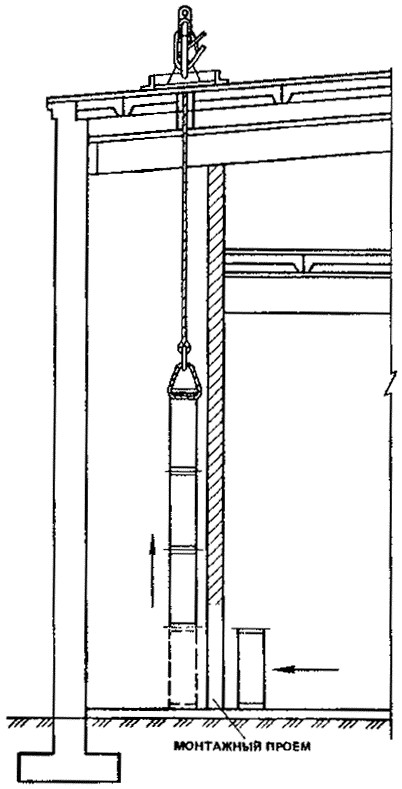
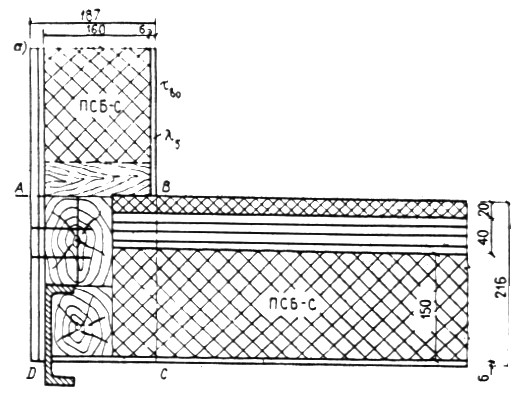
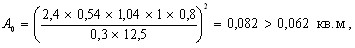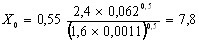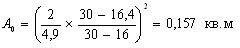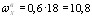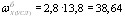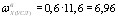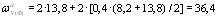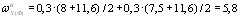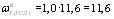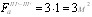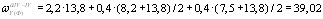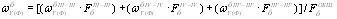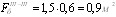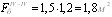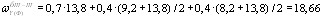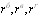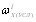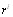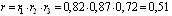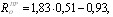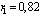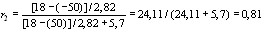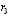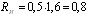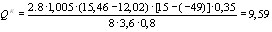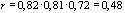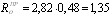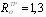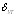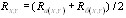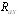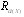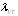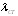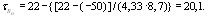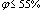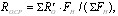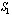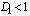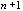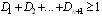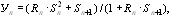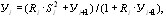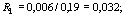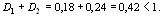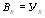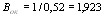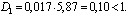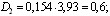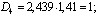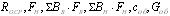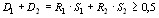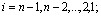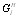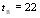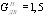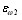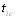Центральный                        Ордена Трудового

научно-исследовательский                Красного Знамени

и проектно-экспериментальный                научно-исследовательский

институт промышленных зданий                Институт бетона

и сооружений (ЦНИИпромзданий)                и железобетона (НИИЖБ)

Госстроя СССР                        Госстроя СССР

ПОСОБИЕ

по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов

(к СНиП 2.03.01-84)

ЧАСТЬ 1

Утверждено приказом ЦНИИпромзданий Госстроя СССР

от 30 ноября 1984 г. № 106а

Москва • Центральный институт типового проектирования • 1988

Рекомендовано к изданию решением секции несущих конструкций научно-технического совета ЦНИИпромзданий Госстроя СССР.

Пособие состоит из двух частей, издаваемых отдельными книгами.

Часть 1. Разд. 1. Общие указания.

Разд. 2. Материалы для железобетонных конструкций.

Разд. 3. Расчет элементов железобетонных конструкций по предельным состояниям первой группы.

Часть II. Разд. 4. Расчет элементов железобетонных конструкций по предельным состояниям второй группы.

Разд. 5. Конструктивные требования.

Содержит требования СНиП 2.03.01-84, относящиеся к проектированию указанных конструкций, положения, детализирующие эти требования, приближенные способы расчета, дополнительные указания, необходимые для проектирования, а также примеры расчета.

Для инженерно-технических работников проектных организаций, а также студентов строительных вузов.

При пользовании Пособием следует учитывать утвержденные изменения строительных норм и правил и государственных стандартов, публикуемые в журнале «Бюллетень строительной техники», «Сборнике изменений к строительным нормам и правилам» Госстроя СССР и информационном указателе «Государственные стандарты СССР» Госстандарта.

ПРЕДИСЛОВИЕ

Настоящее Пособие (ч. I и II) содержит положения по проектированию предварительно напряженных железобетонных конструкций промышленных, гражданских и сельскохозяйственных зданий и сооружений, выполняемых из тяжелых и легких бетонов.

В Пособии приведены требования СНиП 2.03.01-84, относящиеся к проектированию указанных конструкций, положения, детализирующие эти требования, приближенные способы расчета, а также дополнительные указания, необходимые для проектирования. Соответствующие номера пунктов и таблиц СНиП 2.03.01-84 указаны в скобках.

Каждый раздел Пособия сопровождается примерами расчета элементов наиболее типичных случаев, встречающихся в практике проектирования. Кроме того, в прил. 1 приведен комплексный пример расчета предварительно напряженной конструкции.

Пособие может быть использовано при проектировании как предварительно напряженных конструкций, так и конструкций без предварительного напряжения. Однако ряд положений по расчету и конструированию, касающихся элементов или их частей, как правило выполняемых без предварительного напряжения, в Пособии не приведен (расчет и конструирование коротких консолей, подрезок, закладных деталей, воспринимающих внешнюю нагрузку, расчеты на продавливание и отрыв и т. п.). Эти материалы приведены в «Пособии по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов, выполняемых без предварительного напряжения арматуры» (М., ЦИТП Госстроя СССР, 1986).

В Пособии не приведены особенности проектирования статически неопределимых и сборно-монолитных конструкций, а также некоторых специальных сооружений (труб, силосов и др.), и в частности не рассмотрены вопросы, связанные с определением усилий в этих конструкциях. Эти вопросы освещаются в специальных пособиях и рекомендациях.

Все единицы физических величин в Пособии соответствуют «Перечню единиц физических величин, подлежащих применению в строительстве». При этом силы выражаются в ньютонах (Н) или в килоньютонах (кН); моменты сил — в кН•м или Н•мм; линейные размеры — в мм (в основном для сечений элементов) или в м (для длин элементов или их участков); напряжения, сопротивления, модули упругости — в мегапаскалях (МПа); распределенные нагрузки и усилия — в кН/м или Н/мм. Поскольку МПа = Н/мм2, при использовании в примерах расчета формул, включающих в себя величины в МПа (напряжения, сопротивления и т. п.), остальные величины приводятся только в Н и мм (мм2).

В таблицах нормативные и расчетные сопротивления и модули упругости материалов приведены в МПа и в кгс/см2.

В Пособии использованы буквенные обозначения и индексы к ним в соответствии с СТ СЭВ 1565-79 (см. прил. 3).

Разработано ЦНИИпромзданий Госстроя СССР (Б.Ф.Васильев, И.К.Никитин, А.Г.Королькова, канд. техн. наук Л.Л.Лемыш) и НИИЖБ Госстроя СССР (доктора техн. наук [А.А.Гвоздев], Ю.П.Гуща, А.С.Залесов, Г.И.Бердичевский, проф. Ю.В.Чиненков, кандидаты техн. наук Р.Л.Серых, Е.А.Чистяков, Л.К.Руллэ, [А.В.Яшин], Т.И.Мамедов, С.А.Мадатян, Н.А.Маркаров, Н.М.Мулин, Н.А.Корнев, Т.А.Кузьмич) с участием НИЛ ФХММ и ТП Главмоспромстройматериалов (д-р техн.  наук С.Ю.Цейтлин, Е.З.Ерманок), КГБ Мосоргстройматериалов (канд. техн. наук В.С.Щукин).

1. ОБЩИЕ УКАЗАНИЯ

ОСНОВНЫЕ ПОЛОЖЕНИЯ

1.1. Настоящее Пособие распространяется на проектирование предварительно напряженных железобетонных конструкций из тяжелых, мелкозернистых и легких бетонов, предназначенных для работы в условиях неагрессивной среды при систематическом воздействии температур не выше 50 °С и не ниже минус 70 оС.

П р и м е ч а н и я: 1. Настоящее Пособие не распространяется на проектирование железобетонных конструкций гидротехнических сооружений, мостов, транспортных тоннелей, труб под насыпями, покрытий автомобильных дорог и аэродромов, а также самонапряженных конструкций.

2. Определение терминов «бетоны тяжелые», «бетоны мелкозернистые» и «бетоны легкие» см. ГОСТ 25192-82. В настоящем Пособии термин «легкие бетоны» включает в себя только бетоны плотной структуры.

1.2. Предварительное напряжение железобетонных конструкций применяется в целях:

снижения расхода стали путем использования арматуры высокой прочности;

увеличения сопротивления конструкций образованию трещин в бетоне и ограничения их раскрытия;

повышения жесткости и уменьшения деформаций конструкций;

обжатия стыков элементов сборных конструкций;

повышения выносливости конструкций, работающих под воздействием многократно повторяющейся нагрузки;

уменьшения расхода бетона и снижения веса конструкций за счет применения бетона высоких классов.

1.3. Предварительное напряжение создается двумя основными способами:

натяжением арматуры на упоры формы или стенда;

натяжением арматуры на затвердевший бетон.

Натяжение арматуры на упоры производится механическим, электротермическим или электротермомеханическим способом, а натяжение арматуры на бетон, —  как правило, механическим способом.

При натяжении на упоры применяются стержневая арматура, высокопрочная проволока в виде пакетов и арматурные канаты. При натяжении на бетон применяются высокопрочная проволока в виде пучков и арматурные канаты. Кроме того, проволока и арматурные канаты небольших диаметров могут натягиваться на упоры форм или бетон путем непрерывной намотки.

1.4 (1.4). Элементы сборных конструкций должны отвечать условиям механизированного изготовления на специализированных предприятиях.

Целесообразно укрупнять элементы сборных конструкций, насколько это позволяют грузоподъемность монтажных механизмов, условия изготовления и транспортирования.

1.5 (1.8). Расчетная зимняя температура наружного воздуха принимается как средняя температура воздуха наиболее холодной пятидневки в зависимости от района строительства согласно СНиП 2.01.01-82. Расчетные технологические температуры устанавливаются заданием на проектирование.

Влажность воздуха окружающей среды определяется как средняя относительная влажность наружного воздуха наиболее жаркого месяца в зависимости от района строительства согласно СНиП 2.01.01-82 или как относительная влажность внутреннего воздуха помещений отапливаемых зданий.

ОСНОВНЫЕ РАСЧЕТНЫЕ ТРЕБОВАНИЯ

1.6 (1.10). Предварительно напряженные железобетонные конструкции должны удовлетворять требованиям расчета по несущей способности (предельные состояния первой группы) и по пригодности к нормальной эксплуатации (предельные состояния второй группы).

а) Расчет по предельным состояниям первой группы должен обеспечивать конструкции от:

хрупкого, вязкого или иного характера разрушения (расчет по прочности с учетом в необходимых случаях прогиба конструкции перед разрушением) ;

усталостного разрушения (расчет на выносливость конструкций, находящихся под воздействием многократно повторяющейся нагрузки — подвижной или пульсирующей: подкрановых балок, шпал, перекрытий под некоторые неуравновешенные машины и т.п.);

потери устойчивости формы конструкции или ее положения;

разрушения под совместным воздействием силовых факторов и неблагоприятных влияний внешней среды (периодического или постоянного воздействия агрессивной среды, попеременного замораживания и оттаивания, пожара и т. п.).

б) Расчет по предельным состояниям второй группы должен обеспечивать конструкции от:

образования трещин, а также их чрезмерного или продолжительного раскрытия (если по условиям эксплуатации образование или продолжительное раскрытие трещин недопустимо);

чрезмерных перемещений (прогибов, углов перекоса и поворота, колебаний).

П р и м е ч а н и е. Расчет на устойчивость формы или положения конструкции, а также расчеты на совместное воздействие силовых факторов и неблагоприятных влияний внешней среды выполняются по соответствующим нормативным документам, пособиям или литературным источникам.

1.7 (1.11). Расчет по предельным состояниям конструкции в целом, а также отдельных ее элементов должен, как правило, производиться для всех стадий — изготовления, транспортирования, возведения и эксплуатации, при этом расчетные схемы должны отвечать принятым конструктивным решениям.

1.8 (1.12). Значения нагрузок и воздействий, коэффициентов надежности по нагрузке, коэффициентов сочетаний, а также подразделение нагрузок на постоянные и временные должны приниматься в соответствии с требованиями СНиП 2.01.07-85.

Значения нагрузок необходимо умножать на коэффициенты надежности по назначению, принимаемые согласно «Правилам учета степени ответственности здании и сооружений при проектировании конструкций»1, утвержденным Госстроем СССР.

1 См. Бюллетень строительной техники, 1981, №7.

Нагрузки, учитываемые при расчете по предельным состояниям второй группы (эксплуатационные), следует принимать согласно указаниям пп. 1.10 и 1.14. При этом к длительным нагрузкам относится также часть полного значения кратковременных нагрузок, оговоренных в СНиП 2.01.07-85, а вводимую в расчет кратковременную нагрузку следует принимать уменьшенной на величину, учтенную в длительной нагрузке (например, если снеговая нагрузка для III района составляет s = 1000 Н/м2, то снеговая длительная нагрузка будет равна sl = 0,3 • 1000 = 300 Н/м2, а снеговая кратковременная нагрузка - ssh = 1000 — 300 = 700 Н/м2). Коэффициенты сочетаний относятся к полному значению кратковременных нагрузок.

1.9 (1.13). При расчете элементов сборных конструкций на воздействие усилий, возникающих при их подъеме, транспортировании и монтаже, нагрузку от веса элемента следует вводить в расчет с коэффициентом динамичности, равным:

при транспортировании — 1,60;

при подъеме и монтаже — 1,40.

В этом случае учитывается также коэффициент надежности по нагрузке.

1.10 (1.16). К трещиностойкости конструкций (или их частей) предъявляются требования соответствующих категорий в зависимости от условий, в которых они работают, и от вида применяемой арматуры:

а) 1-я категория — образование трещин не допускается;

б) 2-я категория — допускается ограниченное по ширине непродолжительное раскрытие трещин acrc1 при условии обеспечения их последующего надежного закрытия (зажатия);

в) 3-я категория — допускается ограниченное по ширине непродолжительное acrc1 и продолжительное аcrc2 раскрытие трещин.

Под непродолжительным раскрытием трещин понимается их раскрытие при совместном действии постоянных, длительных и кратковременных нагрузок, а под продолжительным — только постоянных и длительных нагрузок.

Категории требований к трещиностойкости железобетонных конструкций, а также значения предельно допустимой ширины раскрытия трещин в условиях неагрессивной среды приведены: для ограничения проницаемости конструкций — в табл. 1а, для обеспечения сохранности арматуры — в табл. 1б.

Таблица 1а (1)

Таблица 1б (2)

П р и м е ч а н и я: 1. Для конструкций, рассчитываемых на выносливость, предельно допустимая ширина раскрытия трещин принимается равной соответствующим значениям ширины продолжительного раскрытия трещин acrc2.

2. При использовании канатов класса К-7 диаметр проволоки принимается равным одной трети диаметра каната.

3. В обозначениях классов арматуры А-III, A-IV, A-V и A-VI подразумеваются также все разновидности термически и термомеханически упрочненной арматуры соответствующего класса (см. п. 2.15).

Эксплуатационные нагрузки, учитываемые при расчете железобетонных конструкций по образованию трещин, их раскрытию или закрытию, должны приниматься согласно табл. 2.

Таблица 2 (3)

* Коэффициент надежности по нагрузке γf принимается как и при расчете по прочности.

** При проверке зоны, растянутой от усилия обжатия, γsp > 1,0.

П р и м е ч а н и я: 1. Длительные и кратковременные нагрузки принимаются с учетом указаний п. 1.8.

2. Особые нагрузки учитываются в расчете по образованию трещин в тех случаях, когда наличие трещин приводит к катастрофическому положению (взрыву, пожару и т. п.).

3. Коэффициент точности натяжения γsp определяется согласно п. 1.18.

4. При действии многократно повторяющихся нагрузок принимаются те же коэффициенты надежности по нагрузке γf, что и при расчете на выносливость, согласно СНиП 2.01.07-85 (т.е. для всех элементов, кроме подкрановых балок, γf=1,0).

5. Для участков в пределах длины зоны передачи напряжений (см. п. 2.26) всегда принимается γsp < 1,0 независимо от категории требований к трещиностойкости.

Если в конструкциях или их частях, к трещиностойкости которых предъявляются требования 2-й и 3-й категорий, трещины не образуются при соответствующих нагрузках, указанных в табл. 2, их расчет по непродолжительному раскрытию и закрытию трещин (для 2-й категории) или по непродолжительному и продолжительному раскрытию трещин (для 3-й категории) не производится.

Указанные категории требований к трещиностойкости железобетонных конструкций относятся к трещинам, нормальным и наклонным к продольной оси элемента.

Категория требований к трещиностойкости различных зон элемента устанавливается, если рассматриваются:

а) нормальные трещины — по виду и классу продольной арматуры рассматриваемой зоны;

б) наклонные трещины - по виду и классу поперечной и отогнутой арматуры, а также по виду и классу продольной арматуры в случаях, когда в местах ее расположения по высоте сечения возможно образование наклонных трещин (см. п. 4.9).

Во избежание раскрытия продольных трещин следует принимать конструктивные меры (устанавливать соответствующую поперечную арматуру) и, кроме того, ограничивать значения сжимающих напряжении в бетоне в стадии предварительного обжатия (см. п. 1.22).

П р и м е ч а н и е. К предварительно напряженным конструкциям без сцепления арматуры с бетоном должны предъявляться требования 1-й категории.

1.11 (1.17). На концевых участках предварительно напряженных элементов с арматурой без анкеров в пределах длины зоны передачи напряжений (см. п. 2.26) не допускается образование трещин при действии постоянных, длительных и кратковременных нагрузок, вводимых в расчет с коэффициентом γf=1,0.

Указанное требование допускается не учитывать для части сечения, расположенной по его высоте от уровня центра тяжести приведенного сечения до растянутой от действия усилия предварительного обжатия грани, если в этой части отсутствует напрягаемая арматура без анкеров.

1.12 (1.18). В случае, если в сжатой при эксплуатационных нагрузках зоне предварительно напряженных элементов, согласно расчету в стадии изготовления, транспортирования и возведения, образуются трещины, нормальные к продольной оси, следует учитывать снижение трещиностойкости растянутой при эксплуатации зоны элементов, а также увеличение их кривизны. Для элементов, рассчитываемых на воздействие многократно повторяющейся нагрузки, образование таких трещин не допускается.

1.13 (1.19). Для железобетонных слабоармированных элементов, характеризуемых тем, что их несущая способность исчерпывается одновременно с образованием трещин в бетоне растянутой зоны, площадь сечения продольной растянутой арматуры должна быть увеличена по сравнению с требуемой из расчета по прочности не менее чем на 15 %.

Такое увеличение армирования следует производить при выполнении условий:

       Mcrc ≥ Mu ;       ξ < ξR ,          (1)

где Мcrc —  момент трещинообразования, определяемый согласно п. 4.2 с заменой Rbt,ser на 1,2 Rbt,ser и при γsp=1,0;

Мu — момент, соответствующий исчерпанию несущей способности, определяемой согласно пп.3.1—3.18, 3.35—3.53; для внецентренно сжатых и растянутых элементов значения Мu определяются относительно оси, проходящей через ядровую точку, наиболее удаленную от растянутой зоны (см. п. 4.2);

ξ, ξR — соответственно относительная высота сжатой зоны и ее граничное значение, определяемые при расчете по прочности.

1.14 (1.20). Прогибы элементов железобетонных конструкций не должны превышать предельно допустимых значений, устанавливаемых с учетом следующих требований:

а) технологических (условия нормальной работы кранов, технологических установок, машин и т.п.);

б) конструктивных (влияние соседних элементов, ограничивающих деформации, необходимость выдерживания заданных уклонов и т. п.);

в) эстетических (впечатление людей о пригодности конструкции).

Значения предельно допустимых прогибов приведены в табл. 3.

Таблица 3 (4)

Обозначение, принятое в табл. 3: l — пролет балок или плит; для консолей принимается значение l, равное удвоенному вылету консоли.

П р и м е ч а н и е. Предельно допустимые прогибы по поз. 1 и 5 обусловлены технологическими и конструктивными, а по поз. 2-4 - эстетическими требованиями.

Расчет по деформациям должен производиться при ограничении требований: технологических или конструктивных — на действие постоянных, длительных и кратковременных нагрузок; эстетических — на действие постоянных и длительных нагрузок. При этом принимается γf=1,0.

При действии постоянных, длительных и кратковременных нагрузок прогиб балок или плит во всех случаях не должен превышать 1/150 пролета и 1/75 вылета консоли.

Значения предельно допустимых прогибов могут быть увеличены на высоту строительного подъема, если это не ограничивается технологическими или конструктивными требованиями.

Для не связанных с соседними элементами железобетонных плит перекрытий, лестничных маршей, площадок и т.п. должна производиться дополнительная проверка по зыбкости: добавочный прогиб от кратковременно действующей сосредоточенной нагрузки 1000 Н при наиболее невыгодной схеме ее приложения должен быть не более 0,7 мм.

Если в нижележащем помещении с плоским потолком имеются расположенные поперек пролета элемента l постоянные перегородки, не являющиеся опорами, с расстояниями между ними lp , то прогиб элемента в пределах расстояния lр (отсчитываемый от линии, соединяющей верхние точки осей перегородок) может быть допущен до lp , однако при этом предельный прогиб всего элемента должен быть не более l.

ПРЕДВАРИТЕЛЬНЫЕ НАПРЯЖЕНИЯ В ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЯХ

1.15 (1.23). Предварительные напряжения σsp (σ′sp) в напрягаемой арматуре без учета потерь следует назначать таким образом, чтобы выполнялись условия при способах натяжения:

механическом

       0,32 Rs,ser ≤ σsp ≤ 0,95 Rs,ser ;        (2)

электротермическом и электротермомеханическом

       0,3 Rs,ser + p ≤ σsp ≤ 0,95 Rs,ser - p ;         (3)

где p - допустимое отклонение значения предварительного напряжения, МПа, равное:

        ,        (4)

здесь l - длина натягиваемого стержня (расстояние между наружными гранями упоров), м. При автоматизированном натяжении1 значение числителя 360 во втором члене формулы (4) заменяется на 90.

1 См. «Рекомендации по технологии автоматизированной заготовки и натяжения высокопрочной стержневой арматуры многопустотных настилов». - М., НИИЖБ, 1984.

Кроме того, при электротермическом способе натяжения значения σsp (σ′sp) следует назначать с учетом допустимых температур нагрева согласно «Руководству по технологии изготовления предварительно напряженных железобетонных конструкций» (М., Стройиздат, 1975); в случае отсутствия данных о технологии изготовления конструкций значение σsp принимается не более: для горячекатаных сталей - 700 МПа, для термически упрочненных сталей - 550 МПа.

При наличии перегибов проволочной арматуры напряжения σsp не должны превышать 0,85 Rs,ser.

1.16 (1.25). При расчете предварительно напряженных элементов следует учитывать потери предварительного напряжения арматуры.

При натяжении арматуры на упоры следует учитывать потери:

а) первые - от деформации анкеров, трения арматуры об огибающие приспособления, от релаксации напряжений в арматуре, температурного перепада, деформации форм (при натяжении арматуры на формы), от быстронатекающей ползучести бетона;

б) вторые - от усадки и ползучести бетона.

При натяжении арматуры на бетон следует учитывать потери:

а) первые - от деформации анкеров, трения арматуры о стенки каналов или поверхность бетона конструкции;

б) вторые - от релаксации напряжений в арматуре, усадки и ползучести бетона, смятия бетона под витками арматуры, деформации стыков между блоками (для конструкций, состоящих из блоков).

Потери предварительного напряжения арматуры следует определять по табл. 4, при этом суммарную величину потерь при проектировании конструкций необходимо принимать не менее 100 МПа.

Таблица 4 (5)

П р и м е ч а н и е. Потери предварительного напряжения в напрягаемой арматуре S' определяются так же, как и в арматуре S.

Черт. 1. Схема изменения напряжений в арматуре при наличии трения арматуры о стенки каналов, о поверхность бетона или об огибающие приспособления

1 - натяжное устройство; 2 - анкер; σ4 - потери напряжении от трения

Таблица 5(6)

Таблица 6

1.17 (1.26). При определении потерь предварительного напряжения от усадки и ползучести бетона по поз. 8 и 9 табл. 4 необходимо учитывать следующее:

а) при заранее известном сроке загружения конструкции потери следует умножать на коэффициент φl, определяемый по формуле

        ,        (5)

где t — время, сут, отсчитываемое при определении потерь от ползучести - со дня обжатия бетона и от усадки - со дня окончания бетонирования.

При проектировании стропильных балок и ферм, ригелей перекрытий массового заводского изготовления допускается потери от усадки и ползучести умножать на коэффициент φl при t = 65 сут;

б) для конструкций, предназначенных для эксплуатации при влажности воздуха ниже 40 %, потери должны быть увеличены на 25 %, за исключением конструкций из тяжелого и мелкозернистого бетонов, предназначенных для эксплуатации в климатическом подрайоне IVA согласно СНиП 2.01.01-82 и не защищенных от солнечной радиации, для которых указанные потери увеличиваются на 50 %.

1.18 (1.27). Значение предварительного напряжения в арматуре вводится с коэффициентом точности натяжения арматуры γsp, определяемым по формуле

               γsp = 1 ± Δγsp .        (6)

Знак «плюс» принимается при неблагоприятном влиянии предварительного напряжения (т.е. на данной стадии работы конструкции или на рассматриваемом участке элемента предварительное напряжение снижает несущую способность, способствует образованию трещин и т.п.), знак «минус» - при благоприятном.

Значения Δγsp при механическом способе натяжения арматуры принимаются равными 0,1, а при электротермическом и электротермомеханическом способах натяжения определяются по формуле

       Δγsp = ,        (7)

но принимаются не менее 0,1,

где р, σsp - см. п. 1.15;

np - число стержней напрягаемой арматуры в сечении элемента.

При определении потерь предварительного напряжения арматуры, а также при расчете по раскрытию трещин и по деформациям значение Δγsp допускается принимать равным нулю. При расчете по образованию и закрытию трещин значения γsp определяются с учетом указаний табл. 2.

1.19 (1.28). Усилие предварительного обжатия Р и эксцентриситет его приложения e0р относительно центра тяжести приведенного сечения (черт. 2) определяются по формулам:

       P = σsp Asp + σ′sp A′sp - σs As - σ′s A′s ;        (8)

       e0р = ,        (9)

где σs, σ′s - напряжения в ненапрягаемой арматуре соответственно S и S′, вызванные усадкой и ползучестью бетона;

уsp, у′sp, ys, y′s - расстояния от центра тяжести приведенного сечения до точек приложения равнодействующих усилий соответственно в напрягаемой и ненапрягаемой арматуре S и S′ (см. черт. 2).

Черт. 2. Схема усилий предварительного напряжения арматуры
в поперечном сечении железобетонного элемента

При криволинейной напрягаемой арматуре значения σsp и σ′sp умножают соответственно на cos θ и cos θ′ , где θ и θ' - углы наклона оси арматуры к продольной оси элемента (для рассматриваемого сечения).

Напряжения σsp и σ′sp следует принимать:

а) в стадии изготовления (с учетом подъема и складирования) — с учетом первых потерь;

б) в стадии эксплуатации (включая стадии транспортирования и возведения) - с учетом первых и вторых потерь.

Напряжения σs и σ′s следует принимать численно равными:

в стадии изготовления — потерям напряжений от быстронатекающей ползучести по поз. 6 табл. 4;

в стадии эксплуатации — сумме потерь напряжений от усадки и ползучести бетона по поз. 6, 8 и 9 табл. 4.

Для ненапрягаемой арматуры S′, расположенной при обжатии в растянутой зоне, напряжение σ′s принимается равным нулю.

1.20. Для элементов с напрягаемой арматурой без анкеров на длине зоны передачи напряжений lp значения (σsp) (σ′sp) снижаются путем умножения их на отношение lx / lp, где lx - расстояние от начала зоны передачи напряжения до рассматриваемого сечения.

Значение lр при этом определяют согласно указаниям п. 2.26 с заменой σtp на напряжение σsp, определенное с учетом потерь по поз. 1-5 табл. 4.

Если площадь сечения всей ненапрягаемой арматуры составляет менее 15 % площади всей напрягаемой арматуры, усилие Р для сечений на длине lр допускается снижать путем непосредственного умножения его на lx / lp.

1.21 (1.28). Напряжения в бетоне σb (σbp) в сечениях, нормальных к продольной оси элемента, определяются по правилам расчета упругих материалов по приведенному сечению. При этом усилие предварительного обжатия Р рассматривается как внешняя сила. Для изгибаемых элементов значение σb (σbp)  определяется по формуле

        ,        (10)

где у — расстояние от центра тяжести приведенного сечения до рассматриваемого волокна;

М — изгибающий момент в рассматриваемой стадии работы элемента.

В формуле (10) сжимающие напряжения учитываются со знаком «плюс», а растягивающие - со знаком «минус».

Приведенное сечение включает в себя сечение бетона с учетом ослабления его каналами, пазами и т.п., а также сечение всей продольной (напрягаемой и ненапрягаемой) арматуры, умноженное на отношение α модулей упругости, арматуры и бетона. Если части бетонного сечения выполнены из бетонов разных классов или видов, их приводят к одному классу или виду, исходя из отношения модулей упругости бетона.

Геометрические характеристики приведенного сечения при бетоне одного вида и класса определяют по формулам:

площадь приведенного сечения

       Ared = A + α Asp + α A′sp + α As + α A′s ;        (11)

расстояние от центра тяжести приведенного сечения до растянутого волокна

,        (12)

где S — статический момент сечения бетона относительно растянутой грани;

момент инерции приведенного сечения относительно его центра тяжести

Ired = I + α Asp y2sp + α A′sp y′2sp + α As y2s + α A′s y′2s .        (13)

Обозначения к формулам (12) и (13) — см. черт. 2.

Допускается не уменьшать площадь сечения бетона А, если общая площадь сечения арматуры оставляет не более 0,03 А.

1.22 (1.29). Сжимающие напряжения в бетоне в стадии предварительного обжатия σbp не должны превышать значений (в долях от передаточной прочности бетона Rbp), указанных в табл. 7.

Таблица 7 (7)

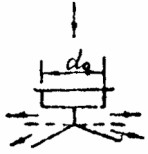
* Для элементов, изготовляемых с постепенной передачей усилий обжатия, при наличии стальных опорных деталей и дополнительной поперечной арматуры, охватывающей все продольные стержни (см. п. 5.46) при ≥ 0,5% (где Asw1 и s - площадь сечения и шаг огибающего хомута), на длине не менее длины зоны передачи напряжений lp (см. п. 2.26) допускается принимать = 1,00.

П р и м е ч а н и я: 1. Значения σbp / Rbp, указанные в настоящей таблице, для бетона в водонасыщенном состоянии при расчетной температуре воздуха ниже минус 40 °С следует принимать на 0,05 меньше.

2. Расчетные зимние температуры наружного воздуха принимаются согласно указаниям п. 1.5.

3. Для легких бетонов классов В7,5 - В12,5 значения σbp / Rbp следует принимать не более 0,30.

Напряжения σbp определяются на уровне крайнего сжатого волокна бетона с учетом первых потерь предварительного напряжения и при коэффициенте точности натяжения арматуры γsp, равном единице.

1.23 (1.24). Значения напряжений σcon1 и σ′con1 в напрягаемой арматуре соответственно S и S′, контролируемые по окончании натяжения на упоры, принимаются равными σsp и σ′sp (см. п. 1.15) за вычетом потерь по поз. 3 и 4 табл. 4.

Значения напряжений в напрягаемой арматуре S и S′, контролируемые в месте приложения натяжного усилия при натяжении арматуры на затвердевший бетон, принимаются равными соответственно σcon2 и σ′con2, определяемым из условия обеспечения в расчетном сечении напряжений σsp и σ′sp по формулам:

       σcon2 = σsp - α σb ;        (14)

       σ′con2 = σ′sp - α σ′b ;        (15)

где σsp, σ′sp — определяются без учета потерь предварительного напряжения;

σb, σ′b — напряжения в бетоне на уровне арматуры S и S′ (см. п. 1.21) от действия усилия обжатия Р, определенного с учетом первых потерь напряжений.

В конструкциях из легкого бетона классов В7,5—В12,5 значения σcon1 и σcon2 не должны превышать соответственно 550 и 400 МПа.

При применении в элементе нескольких пучков или канатов арматуры, натягиваемых на бетон неодновременно, контролируемые напряжения в каждом из них рекомендуется определять с учетом влияния упругого обжатия, вызванного усилиями пучков или канатов, натягиваемых позднее.

Контролируемые напряжения группы арматуры k определяются в этом случае по формуле

       σcon,k = σcon,2 ± ,        (16)

где σcon,2  — напряжение в арматуре группы k, определяемое по формуле (14);

σbki — среднее по длине арматуры рассматриваемой группы k напряжение в бетоне на уровне ее центра тяжести от упругого обжатия бетона усилием группы арматуры i, натягиваемой позднее;

t - число групп арматуры, натягиваемых позднее группы k.

В формуле (16) при сжимающем напряжении σbki принимают знак «плюс», а при растягивающем — «минус».

Среднее напряжение в бетоне σbki для элемента с переменным по длине поперечным сечением определяется по формуле

       σbki = ,        (17)

где σbki(j) — напряжения в бетоне в среднем сечении j-го участка;

lj — длина j-го участка;

l - длина элемента в пределах рассматриваемого пучка (каната) .

При прямолинейных и параллельных к продольной оси элемента пучках (канатах) и постоянном поперечном сечении элемента значение Σσbki определяют по формуле (10), вычисляя P (и соответствующее значение e0) от всей арматуры, натягиваемой после рассматриваемой группы k.

Примеры расчета

Пример 1. Дано: плита покрытия размером 1,5×6 м; поперечное сечение — по черт. 3; бетон тяжелый класса В25 (Еb = 2,7⋅104 МПа); передаточная прочность бетона Rbp = 17,5 МПа; напрягаемая арматура класса A-IV (Rs,ser = 590 МПа, Es = 19⋅104 МПа) площадью сечения Аsp = 201 мм2 (l ∅ 16), ненапрягаемая арматура сжатая и растянутая класса А-III (Еs = 2⋅104 МПа) площадью сечения Аs = А′s = 50,3 мм2 (l ∅ 8); натяжение арматуры производится на упоры формы электротермическим неавтоматизированным способом; технология изготовления плиты — агрегатно-поточная с применением пропаривания; масса плиты 1,3 т.

Требуется определить значение и точку приложения усилия предварительного обжатия P1 (с учетом первых потерь) и Р2 (с учетом всех потерь) для сечения в середине пролета, принимая максимально допустимое натяжение арматуры.

Черт. 3. К примеру расчета 1

Р а с ч е т.  Ввиду симметрии сечения расчет ведем для половины сечения плиты. Определяем геометрические характеристики приведенного сечения согласно п. 1.21, принимая:

коэффициент α для всей арматуры.

;

A′sp = 0.

Площадь приведенного сечения:

Ared = A + α Asp + α As + α A′s = 730 ⋅ 30 +50 ⋅ 270 +60 ⋅ 270 ⋅ 0,5 +
+ 97,5 ⋅ 15 + 7,4 ⋅ 201+ 7,4 ⋅ 50,3 ⋅ 2 = 47 200 мм2.

Статический момент сечения бетона относительно нижней грани ребра

S = 730 ⋅ 30 ⋅ 285 + 50 ⋅ 2702 ⋅ 0,5 + 60 ⋅ 0,5 2702 + 97,52 ⋅ 15 ⋅ 0,5 =
= 9593 ⋅ 103 мм3.

Расстояние от центра тяжести приведенного сечения до нижней грани ребра:

= 206,7 мм;

ysp = y0 - ap = 206,7 - 35 = 171,7 мм ;

ys = y0 - as = 206,7 - 20 = 186,7 мм ;

y′s = h  - a′s - y0 = 300 - 20 - 206,7  = 73,3 мм .

Момент инерции приведенного сечения:

Ired = I + αAspy2sp + αAsy2s + αA′sy′2s = + 730 ⋅ 30 (285 - 206,7)2+ ++ 50 ⋅ 270 (206,7-135)2 ++ 60 ⋅ 270 ⋅ 0,5 (206,7-180)2 + + 15⋅ 97,5 (206,7 - 48,7)2 + 7,4 ⋅ 201 ⋅ 171,72 +
+ 7,4 ⋅ 50,3 ⋅ 186,72 + 7,4 ⋅ 50,3 ⋅ 73,32 = 3599 ⋅ 105 мм4.

Из условия (3) п. 1.15 определим максимально допустимое значение σsp без учета потерь. При длине натягиваемого стержня l = 6 м

90 МПа.

Тогда σsp = Rs,ser - p = 590 - 90 = 500 МПа.

Определим первые потери по поз. 1—6 табл. 4.

Потери от релаксации напряжений в арматуре при электротермическом способе натяжения стержневой арматуры равны:

σ1 = 0,03 σsp = 0,03 ⋅ 500 = 15 МПа.

При агрегатно-поточной технологии форма с упорами при пропаривании нагревается вместе с изделием, поэтому температурный перепад между ними равен нулю и, следовательно, σ2 = 0.

Потери от деформаций анкеров σ3 и формы σ5 при электротермическом натяжении равны нулю. Поскольку напрягаемая арматура не отгибается, потери от трения арматуры σ4 также равны нулю.

Таким образом, усилие обжатия с учетом потерь по поз. 1-5 табл. 4 РI равно:

PI = Asp (σsp - σ1) = 201 (500 - 15) = 97485 H,

а его эксцентриситет равен:

е0p = ysp = 171,7 мм.

Определим потери от быстронатекающей ползучести бетона согласно поз. 6 табл. 4. Для этого вычислим напряжения в бетоне σbp в середине пролета от действия силы PI и изгибающего момента Mw от веса плиты.

Нагрузка от веса плиты равна (см. п. 2.14):

= 1,083 кН/м.

Тогда        Mw = кН⋅м

(l = 5,7м - расстояние между подкладками при хранении плиты).

Напряжение σbp на уровне арматуры S (т.е. при y = ysp = 171,7 мм) равно:

= 7,95 МПа.

Напряжение σ′bp на уровне арматуры S' (т.е. при у = у's = 73,3 мм) равно:

σ′bp = -0,45 МПа < 0 .

Потери от быстронатекающей ползучести равны:

на уровне арматуры S:

α=0,25 + 0,025Rbp=0,25 + 0,025 ⋅ 17,5=0,69 < 0,8 ;

поскольку =0,45 < α=0,69, то σ6=34 =

=34 ⋅ 0,45=15,3 МПа;

на уровне арматуры S':  поскольку σ′bp < 0, то σ6=0.

Напряжение σsp1 с учетом первых потерь равно:

σsp1=σsp - σ1 - σ6=500 - 15 - 15,3=470 МПа.

Напряжения σs и σ′s принимаем равными потерям напряжений от быстронатекающей ползучести, т.е. σs=15,3 МПа и σ′s=0.

Определим усилие обжатия с учетом первых потерь напряжений P1 и его эксцентриситет e0p1 по формулам (8) и (9):

P1=σsp1 Asp - σs As=470⋅201 - 15,3⋅50,3=93,7 ⋅ 103 Н;

e0p1==171,6 мм.

В соответствии с п. 1.22 проверим максимальное сжимающее напряжение бетона σbp от действия силы Р1, вычисляя его по формуле (10) при у=у0=206,7 мм:

σbp==11,2 МПа

(момент от собственного веса не учитывается).

Поскольку =0,64 < 0,95 (см. табл. 7), требование п. 1.22 выполняется.

Определим вторые потери напряжений по поз. 8 и 9 табл. 4.

Потери от усадки равны σ8=35 МПа.

Потери от ползучести σ9:

на уровне арматуры S:

отношение в целях упрощения расчета принимаем, как при определении σ6, т.е. =0,45;

так как =0,45 < 0,75, то σ9=128α =128⋅1⋅0,45=57,6 МПа;

на уровне арматуры S':  поскольку σ′bp < 0, то σ6=0.

Суммарная величина потерь напряжений:

σ1 + σ6 + σ8 + σ9=15 + 15,3 + 35 + 57,6=122,9 МПа > 100 МПа,

следовательно, согласно п. 1.18, потери не увеличиваем.

Напряжение σsp2 с учетом всех потерь равно:

σsp2=500 - 122,9 ≅ 377,1 МПа.

Усилие от обжатия с учетом всех потерь напряжений P2 определяем по формуле (8), принимая напряжение σs равным сумме потерь от усадки и ползучести, т.е.

σs=15,3 + 35 + 57,6=107,9 МПа.

Поскольку σ′bp < 0, σ′s =0, то

P2=σsp2 Asp - σs As=377,1 ⋅ 201 - 107,9 ⋅ 50,3=70 370 Н.

Эксцентриситет усилия P2 равен:

=
=170,5 мм.

Пример 2. Дано: свободно опертая балка с поперечным сечением по черт. 4; бетон тяжелый класса В35 (Eb=3,1 ⋅ 104 МПа); передаточная прочность бетона Rbp=17,5 МПа; напрягаемая арматура из канатов класса К-7 (Rs,ser=1295 МПа, Es=18 ⋅ 104 МПа) площадью сечения: в растянутой зоне Asp=1699 мм2 (12 ∅ 15), в сжатой зоне A′sp=283мм2 (2 ∅ 15); натяжение производится на упоры стенда механическим способом; бетон подвергается пропариванию; закрепление канатов на упорах с помощью инвентарных зажимов; длина стенда 20 м; масса балки 11,2 т; длина балки l=18 м

Требуется определить величину и точку приложения усилия предварительного обжатия с учетом первых потерь напряжения P1 и с учетом всех потерь P2 для сечения в середине пролета, принимая максимально допустимое натяжение арматуры.

Черт. 4. К примеру расчета 2

Р а с ч е т. Определяем геометрические характеристики приведенного сечения согласно п. 1.21, принимая коэффициент α===5,8 (площадь сечения конструктивной ненапрягаемой арматуры не учитывается ввиду ее малости).

Для упрощения расчета высоту свесов полок усредняем.

Площадь приведенного сечения

Ared =А + αАsp + αА'sp=1500⋅80 + 280⋅240 + 200⋅250 + 5,8 (1699+283)==24,9 ⋅ 104 мм2

Расстояние от центра тяжести сечения арматуры S до нижней грани балки (учитывая, что сечения всех четырех рядов арматуры одинаковой площади)

=125 мм.

Статический момент сечения бетона относительно нижней грани балки

S==18 900 ⋅ 104 мм3.

Расстояние от центра тяжести сечения до нижней грани:

=774 мм ;

ysp=y0 - ap=774 - 125=649 мм ;

y′sр=h  - a′р - y0=1500 - 50 - 774 =676 мм .

Момент инерции приведенного сечения

Ired=I + α Asp y2sp + α A′sр y′2sр = + 80 ⋅ 1500 (774 - 750)2 +

++ 280 ⋅ 240 (1380-774)2 ++ 200 ⋅ 250(774-125)2 +

+ 5,8 ⋅ 1699 ⋅ 6492 + 5,8 ⋅ 283 ⋅ 6762=73800 ⋅ 106 мм4 .

Из условия (2) определим максимально допустимое напряжение σsp без учета потерь:

σsp=0,95 Rs,ser=0,95 ⋅ 1295=1226 МПа.

Определим первые потери напряжений по поз. 1—6 табл. 4:

потери от релаксации напряжений в арматуре

=134 МПа ;

потери от температурного перепада между упорами стенда и бетоном при Δt=65 oС

σ2=1,25 Δt=1,25 ⋅ 65=81 МПа;

потери от деформаций анкеров в виде инвентарных зажимов при Δl=1,25 + 0,15d=1,25 + 0,15 ⋅ 15=3,5 мм и l=20 м

σ3=1,8 ⋅ 105=31,5 МПа;

поскольку напрягаемая арматура не отгибается, потери от трения арматуры отсутствуют, т.е. потери σ4=0.

Потери от деформаций стальной формы отсутствуют, поскольку усилие обжатия передается на упоры стенда, т. е. σ5=0.

Таким образом, усилие обжатия РI, с учетом потерь по поз. 1—5 табл. 4 равно:

PI=(Asp+A′sp) (σsp - σ1 - σ2 - σ3) =(1699+283) × (1226-134-81-31,5)=

=1982 ⋅ 980=1941 ⋅ 103 H=1941 кН.

Точка приложения усилия РI совпадает с центром тяжести всей напрягаемой арматуры, т.е.

=447 мм .

Определим потери от быстронатекающей ползучести бетона согласно поз. 6 табл. 4. Для этого по формуле (10) вычислим напряжения в бетоне σbp в середине пролета от действия силы РI и изгибающего момента Mw от собственного веса балки.

Нагрузка от собственного веса балки (см. п. 2.14) равна:

=6,23 кН/м ,

тогда Мw==238 кН⋅м

(l=17,5м - расстояние между подкладками при хранении балки).

Напряжение σbp на уровне арматуры S (т.е. при у=уsp=649 мм)

=13,3 МПа.

Напряжение σ′bp на уровне арматуры S′ (т.е. при у=y'sp=676 мм):

2,1 МПа > 0.

Потери от быстронатекающей ползучести σ6 равны:

на уровне арматуры S:

α=0,25 + 0,025 Rbp=0,25 + 0,025 ⋅ 17,5=0,69 < 0,8 ;

поскольку =0,77 > α=0,69, то

σ6=34 α + 72 β =34⋅0,69 + 72⋅2,01 (0,77-0,69)=35,0 МПа,

где β=5,25 - 0,185 Rbp=5,25 - 0,185 ⋅ 17,5=2,01 < 2,5, но более 1,1;

на уровне арматуры S′:

σ′6=34 =4,1 МПа.

Напряжение σsp1 с учетом первых потерь равно:

для арматуры S

σsp1=(σsp - σ1 - σ2 - σ3) - σ6=980 - 35=945 МПа;

для арматуры S′

σ′sp1=980 - 4,1=976 МПа.

Определим усилие обжатия с учетом первых потерь P1 и его эксцентриситет e0p1 по формулам (8) и (9):

P1=σsp1 Asp + σ′sp1 A′sp=945 ⋅ 1699 + 976 ⋅ 283=1882 кН ;

e0p1==454 мм.

Определим по формуле (10) максимальное сжимающее напряжение бетона от действия силы P1 без учета собственного веса, принимая у=у0=774 мм:

=16,5 МПа.

Поскольку =0,94 < 0,95, требование п.1.22 выполняется.

Определим вторые потери напряжений по поз. 8 и 9 табл. 4.

Потери от усадки равны σ8=35 МПа.

Потери от ползучести σ9:

для арматуры S:

отношение в целях упрощения расчета принимаем, как при определении σ6, т. е. =0,77;

так как =0,77 > 0,75, то σ9=256α =
=256⋅1 × (0,77 - 0,375)=101 МПа;

для арматуры S′:

=15,4 МПа.

Напряжения σsp с учетом всех потерь равны:

для арматуры S

σsp2=σsp1 - σ8 - σ9=945 - 35 - 101=809 МПа;

для арматуры S'

σ′sp2=σ′sp1 - σ8 - σ9=976 - 35 - 15,4=926 МПа.

Определим усилие обжатия с учетом всех потерь P2 и его эксцентриситет e0p2:

P2=σsp2 Asp + σ′sp2 A'sp=809 ⋅ 1699 + 926 ⋅ 283=1637 ⋅ 103 H=1637 кН;

=437 мм.

2. МАТЕРИАЛЫ ДЛЯ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ

БЕТОН

2.1 (2.3). Для предварительно напряженных железобетонных конструкций следует предусматривать бетоны следующих классов и марок:

а) классов по прочности на сжатие:

тяжелый бетон - В12,5; В15; В20; В25; В30; В35; В40; В45; В50; В55; В60;

мелкозернистый бетон групп:

А - естественного твердения или подвергнутый тепловой обработке при атмосферном давлении на песке с модулем крупности свыше 2,0 — В12,5; В15; В20; В25; В30; В35; В40;

Б - то же, с модулем крупности 2,0 и менее - В12,5; В15; В20; В25; В30;

В - подвергнутый автоклавной обработке - В15; В20; В25; В30; В35; В40; В45; В50; В55; В60;

легкий бетон при марках по средней плотности:

D800, D900 - В7,5*;

D1000, D1100 - B7,5; В10; В12,5*;

D1200, D1300 - B7,5; B10; В12,5; В15*;

D1400, D1500 - B7,5; B10; В12,5; В15; В20*; B25*; В30*;

D1600, D1700 - B7,5; B10; B12,5; В15; В20; В25*; В30*; В35*;

D1800, D1900 - B10; B12,5; B15; В20; В25*; В30*; В35*; В40*;

D2000 - В20; В25; В30; В35*; В40*;

допускается применять промежуточные классы бетона В22,5 и В27,5, обоснованные в установленном порядке;

* Отмеченные классы легкого бетона могут применяться лишь при согласовании с заводом-изготовителем.

6) марок по морозостойкости:

тяжелый и мелкозернистый бетоны - F50; F75; F100; F150; F200; F300; F400; F500;

легкий бетон - F25; F35; F50; F75; F100; F150; F200; F300; F400; F500;

в) марок по водонепроницаемости - W2; W4; W6; W8; W10; W12;

г) марок по средней плотности:

легкий бетон - D800; D900; D1000; D1100; D1200; D1300; D1400; D1500; D1600; D1700; D1800; D1900; D2000;

для тяжелых и мелкозернистых бетонов при отсутствии требований к теплоизоляции марки по средней плотности не нормируются.

П р и м е ч а н и е. Определение понятий «класс бетона» и «марка бетона» см. ГОСТ 25192-82.

2.2 (2.4). Возраст бетона, отвечающий его классу по прочности на сжатие, назначается при проектировании исходя из возможных реальных сроков загружения конструкции проектными нагрузками, способа возведения, условий твердения бетона. При отсутствии этих данных класс бетона устанавливается в возрасте 28 сут.

Значение отпускной прочности бетона в элементах сборных конструкций следует назначать в соответствии с ГОСТ 13015.0-83 и стандартами на конструкции конкретных видов.

2.3 (2.6). Класс бетона, в котором расположена напрягаемая арматура, следует принимать не ниже указанного в табл. 8.

Таблица 8 (8)

П р и м е ч а н и е. Классы арматуры приведены в п. 2.15.

Передаточная прочность бетона Rbp назначается не менее 11 МПа, а при стержневой арматуре класса A-VI, арматурных канатах классов К-7 и К-19, а также проволочной арматуре без высаженных головок — не менее 15,5 МПа. Передаточная прочность, кроме того, должна составлять не менее 50 % принятого класса бетона.

Для конструкций, рассчитываемых на воздействие многократно повторяющейся нагрузки, при проволочной арматуре и стержневой арматуре класса A-IV независимо от диаметра, а также класса A-V диаметром 10-18 мм минимальные значения класса бетона, приведенные в табл. 8, должны увеличиваться на одну ступень, равную 5 МПа, с соответствующим повышением минимальной передаточной прочности.

Для стенок монолитных круглых резервуаров и труб при натяжении только спиральной (или кольцевой) арматуры допускается применение бетона класса В12,5 и передаточной прочности Rbp=10 МПа.

При проектировании ограждающих однослойных сплошных конструкций, выполняющих функции теплоизоляции, допускается при относительной величине обжатия бетона σbp / Rbp (см. п. 1.22) не более 0,3 и напрягаемой арматуре класса A-IV диаметром не более 14 мм использование легкого бетона классов В7,5—В12,5; при этом передаточная прочность бетона Rbp должна составлять не менее 80 % класса бетона.

В целях недопущения перерасхода цемента при применении нормативного цикла термовлажностной обработки изделия (13—15 ч) рекомендуется назначать передаточную прочность бетона в долях от принятого класса не более: 0,65 для классов В20—В35 и 0,7 для прочих классов.

П р и м е ч а н и е. Передаточная прочность бетона Rbp (прочность бетона к моменту обжатия) определяется в соответствии с государственными стандартами с обеспеченностью 0,95.

2.4 (2.7). Мелкозернистый бетон без специального обоснования не допускается применять для железобетонных конструкций, подвергающихся воздействию многократно повторяющейся нагрузки, а также для конструкций пролетом более 12 м при армировании проволочной арматурой классов В-II, Вр-II, К-7 и К-19.

Класс мелкозернистого бетона, применяемого для защиты от коррозии и обеспечения сцепления с бетоном напрягаемой арматуры, расположенной в пазах и на поверхности конструкции, должен быть не ниже В12,5, а для инъекции каналов — не ниже В25.

2.5 (2.8). Для замоноличивания стыков элементов сборных железобетонных конструкций класс бетона следует устанавливать в зависимости от условий работы соединяемых элементов, но принимать не ниже В7,5.

2.6 (2.9). Марки бетона по морозостойкости и водонепроницаемости железобетонных конструкций в зависимости от режима их эксплуатации и значений расчетных зимних температур наружного воздуха в районе строительства должны приниматься:

для конструкций зданий и сооружений (кроме наружных стен отапливаемых зданий) - не ниже указанных в табл. 9;

для наружных стен отапливаемых зданий - не ниже указанных в табл. 10.

Таблица 9 (9)

* Для тяжелого и мелкозернистого бетона марки по морозоустойчивости не нормируются.

П р и м е ч а н и я: 1. Марки бетона по морозостойкости и водонепроницаемости для конструкций и сооружений водоснабжения и канализации, а также для. свай и свай-оболочек следует назначать согласно требованиям соответствующих нормативных документов.

2. Расчетные зимние температуры наружного воздуха принимаются согласно указаниям п. 1.5.

Таблица 10 (10)

П р и м е ч а н и я: 1. При наличии паро- и гидроизоляции марки по морозостойкости, указанные в настоящей таблице, снижаются на одну ступень.

2. Расчетная зимняя температура наружного воздуха принимается согласно указаниям п. 1.5.

2.7 (2.10). Для замоноличивания стыков элементов сборных конструкций, которые в процессе эксплуатации или монтажа могут подвергаться воздействию отрицательных температур наружного воздуха, следует применять бетоны проектных марок по морозостойкости и водонепроницаемости не ниже принятых для стыкуемых элементов.

2.8. Для легких бетонов марки по средней плотности назначаются в соответствии с табл. 11.

Таблица 11

Нормативные и расчетные характеристики бетона

2.9 (2.11). Нормативными сопротивлениями бетона являются сопротивление осевому сжатию призм (призменная прочность) Rbn и сопротивление осевому растяжению Rbtn.

Нормативные сопротивления бетона Rbn и Rbtn в зависимости от класса бетона В даны в табл. 12.

Таблица 12 (12)

Окончание табл. 12 (12)

* Для мелкозернистого бетона группы Б (см. п. 2.1) значения Rbtn и Rbt.ser уменьшаются на 15 %.

** Для керамзитоперлитобетона на вспученном перлитовом песке значения Rbtn и Rbt.ser уменьшаются на 15%.

2.10 (2.11, 2.13). Расчетные сопротивления бетона для предельных состояний первой группы Rb и Rbt определяются делением нормативных сопротивлений на коэффициенты надежности по бетону, принимаемые равными: при сжатии γbc=1,3; при растяжении γbt=1,5.

Расчетные сопротивления бетона Rb и Rbt снижаются (или повышаются) умножением на коэффициенты условий работы бетона γbi, учитывающие длительность действия, многократную повторяемость нагрузки, условия и стадию работы конструкции, способ ее изготовления и т.п.

Расчетные сопротивления бетона для предельных состояний второй группы Rb,ser и Rbt,ser принимаются равными нормативным сопротивлениям и входят в расчет с коэффициентом условий работы γb=1,0, за исключением случаев, указанных в пп. 4.8, 4.9 и 4.13.

Значения расчетных сопротивлений бетонов (с округлением) в зависимости от их классов по прочности на сжатие приведены: для предельных состояний первой группы — в табл. 13, для предельных состояний второй группы — в табл. 12.

Таблица 13

Окончание табл. 13

* Для мелкозернистого бетона группы Б (см. п. 2.1) значения Rbt снижаются на 15%.

** Для керамзитоперлитобетона на вспученном перлитовом песке значения Rbt снижаются на 15 %.

В расчетные сопротивления, приведенные в табл. 13, включен коэффициент условий работы γb2, учитывающий влияние длительного действия нагрузок и условия нарастания прочности бетона во времени; порядок использования коэффициентов γb2 в расчете приведен в п. 3.1.

Расчетные сопротивления, приведенные в табл. 13, в соответствующих случаях следует умножать на коэффициенты условий работы, приведенные в табл. 14.

Таблица 14 (15)

П р и м е ч а н и я: 1. Коэффициенты γb1 и γb7 по поз. 1 и 4 должны учитываться при определении расчетных сопротивлений бетона Rb и Rbt, а коэффициенты γb6, γb8 и γb12 - только при определении Rb.

2. Для конструкций, находящихся под воздействием многократно повторяющейся нагрузки, коэффициент γb1 учитывается только при расчете на выносливость и по образованию трещин.

Таблица 15 (17)

П р и м е ч а н и я:  1. Расчетная зимняя температура наружного воздуха принимается согласно п. 1.5.

2. При превышении марки бетона по морозостойкости по сравнению с требуемой согласно табл. 9 коэффициенты настоящей таблицы могут быть увеличены нас 0,05 соответственно каждой ступени превышения, однако не могут быть более единицы.

2.11 (2.14). Значения начального модуля упругости бетона Eb при сжатии и растяжении назначаются по табл. 16.

Таблица 16 (18)

Окончание табл. 16 (18)

П р и м е ч а н и я: 1. Группы мелкозернистого бетона см. п. 2.1.

2. Для легких бетонов при промежуточных значениях марок бетона по средней плотности начальные модули упругости бетона принимаются по линейной интерполяции.

3. Для легкого бетона табличные значения Eb даны при эксплуатационной весовой влажности бетона wусл, составляющей для бетона классов: В12,5 и выше - 5 %, В7,5 и В10 - 10 %. Если для бетона классов В7,5 и В10 весовая влажность конструкции w, %, определенная согласно указаниям СНиП II-3-79*, существенно превышает указанную влажность 10%, значения Eb при необходимости можно несколько увеличить, определяя их по настоящей таблице при условной марке по средней плотности, равной , где D′ - принятая в проекте марка по средней плотности.

Для тяжелого бетона, подвергнутого автоклавной обработке, значения Eb, указанные в табл. 16 для бетона естественного твердения, следует умножать на коэффициент 0,75.

Для не защищенных от солнечной радиации конструкций, предназначенных для работы в климатическом подрайоне IVA согласно СНиП 2.01.01-82, значения Eb, указанные в табл. 16, следует умножать на коэффициент 0,85.

Для бетонов, подвергающихся попеременному замораживанию и оттаиванию (см. поз. 1а и 1б табл. 9), значения Eb, указанные в табл. 16, следует умножать на коэффициент условий работы γb6, принимаемый по табл. 15.

2.12 (2.16). Начальный коэффициент поперечной деформации бетона ν (коэффициент Пуассона) принимается равным 0,2, а модуль сдвига бетона G - равным 0,4 Eb.

2.13 (2.15). Коэффициент линейной температурной деформации αbt при изменении температуры от минус 40 до плюс 50 oС принимается равным 1-10-5 °С-1, за исключением конструкций из легкого бетона при мелком пористом заполнителе, для которых коэффициент αbt принимается равным 0,7-10-5 °С-1.

2.14. Для определения массы железобетонной конструкции плотность бетона принимается равной: для тяжелого бетона - 2400 кг/м3, для мелкозернистого бетона - 2200 кг/м3, для легкого бетона - марке бетона по средней плотности D (кг/м3), умноженной для бетона классов: В 12,5 и выше - на 1,05, В10 и В7,5 - на 1 + , где w - весовая влажность при эксплуатации, %, определенная согласно СНиП II-3-79*; допускается w принимать равной 10%. При расчете конструкции в стадии изготовления и транспортирования плотность легкого бетона определяется с учетом отпускной объемной влажности ω по формуле D + 1000, где ω=10 и 15% для бетона соответственно классов В12,5 и выше и классов В10 и ниже. Плотность железобетона при содержании арматуры 3 % и менее может приниматься превышающей плотность бетона на 100 кг/м3; при содержании арматуры более 3 % плотность определяется как сумма масс бетона и арматуры на единицу объема железобетонной конструкции. При этом масса 1 м арматурной, полосовой, угловой и фасонной стали в кг принимается по прил. 4, а также по государственным стандартам. Для определения нагрузки от собственного веса. удельный вес конструкции в кН/м3 допускается принимать равным 0,01 от плотности в кг/м3.

АРМАТУРА

2.15 (2.17). Для армирования железобетонных конструкций должна применяться арматура, отвечающая требованиям соответствующих государственных стандартов или технических условий (табл. 17) и принадлежащая одному из следующих видов:

стержневая арматурная сталь:

а) горячекатаная — гладкая класса А-I, периодического профиля классов А-II, А-III, A-IV, A-V, A-VI;

б) термически и термомеханически упрочненная — периодического профиля классов Ат-IIIС, Ат-IVC, Aт-IVK, Ат-V, Ат-VCK, Ат-VI, Ат-VIK ;

в) упрочненная вытяжкой класса А-IIIв;

проволочная арматурная сталь:

г) арматурная холоднотянутая проволока:

обыкновенная — периодического профиля класса Вр-I;

высокопрочная — гладкая класса В-II, периодического профиля класса Вр-II;

д) арматурные канаты — спиральные семипроволочные класса К-7, 19-проволочные класса К-19.

В качестве конструктивной арматуры допускается также применять обыкновенную гладкую проволоку класса В-I.

П р и м е ч а н и я : 1. В обозначениях термически и термомеханически упрочненной стержневой арматуры буква К означает арматуру с повышенной стойкостью к коррозионному растрескиванию под напряжением; буква С - свариваемую арматуру; буквы СК — арматуру свариваемую и повышенной стойкости к коррозионному растрескиванию под напряжением.

2. Классы горячекатаной, термически и термомеханически упрочненной арматуры с одним и тем же номером имеют одинаковые механические свойства, поэтому в дальнейшем, если для расчетов нет необходимости указывать конкретный вид стержневой арматуры, используются обозначения соответствующих классов горячекатаной арматуры: например, под классом A-V подразумеваются все виды стержневой арматуры соответствующего класса, т.е. A-V, Ат-V, Ат-VCK.

3. В обозначении горячекатаной стержневой арматуры класса А-II специального назначения добавляется буква «с» - Ас-II.

4. В тексте для краткости используются следующие термины: «стержень» - для обозначения арматуры любого диаметра, вида и профиля независимо от того, поставляется ли она в прутках или мотках (бунтах); «диаметр» (d), если не оговорено особо, означает номинальный диаметр стержня.

Таблица 17 (Обязательное приложение 1)

Окончание табл. 17 (обязательного приложения 1)

1 Допускается применять только в вязаных каркасах и сетках.

2 Следует применять только в виде целых стержней мерной длины.

П р и м е ч а н и я: 1. В таблице знак «плюс» означает допускается, знак «минус» — не допускается.

2. Расчетная температура принимается согласно указаниям п. 1.5.

3. В данной таблице нагрузки следует относить: к динамическим, если доля этих нагрузок при расчете конструкций по прочности превышает 0,1 статической нагрузки; к многократно повторяющимся - нагрузки, при которых коэффициент условий работы арматуры γs3 < 1,0 (см. табл. 36).

4. Качество упрочненной вытяжкой арматуры класса А-Шв регламентируется прил. 2 «Руководства по технологии изготовления предварительно напряженных железобетонных конструкций» (М., Стройиздат, 1975).

2.16. Применяемая в железобетонных конструкциях арматура имеет предел текучести:

физический (стержневая классов А-I, А-II и АIII);

условный, равный величине напряжений, соответствующих остаточному относительному удлинению 0,2 % (стержневая классов A-IV и выше, проволочная арматура классов В-II, Bp-II, К-7 и К-19).

Упрочненная вытяжкой арматура класса А-IIIв и обыкновенная арматурная проволока класса Вр-I по особенностям расчета условно отнесены к арматуре, имеющей физический предел текучести.

2.17 (2.21). В качестве напрягаемой арматуры предварительно напряженных железобетонных элементов:

при длине до 12 м включ.

следует преимущественно применять

а) термическя и термомеханически упрочненную арматуру классов Ат-VI и Ат-V;

допускается применять:

б) арматурную проволоку классов В-II, Bp-II и арматурные канаты классов К-7 и К-19;

в) горячекатаную арматуру классов A-VI, A-V, A-IV;

г) стержневую арматуру класса А-IIIв;

при длине элементов свыше 12 м:

следует преимущественно применять:

д) арматурную проволоку классов В-II и Bp-II и арматурные канат классов К-7 и К-19;

е) горячекатаную арматуру классов A-VI и A-V;

допускается применять

ж) стержневую арматуру классов A-IV, Ат-IVC и А-IIIв.

П р и м е ч а н и е. Для армирования предварительно напряженных конструкций из легкого бетона классов В7,5 - В12,5 следует преимущественно применять стержневую арматуру класса A-IV.

2.18. (2.22). В качестве напрягаемой арматуры предварительно напряженных элементов, находящихся:

под давлением газов, жидкостей или сыпучих тел:

следует преимущественно применять:

а) арматурную проволоку классов В-II, Bp-II и арматурные канаты классов К-7 и К-19;

б) стержневую арматуру классов A-V и A-VI;

допускается применять

в) стержневую арматуру классов A-IV и А-IIIв;

под воздействием агрессивной среды следует преимущественно применять горячекатаную арматуру класса A-IV и термомеханически упрочненную классов Ат-VIK, Ат-VCK, Ат-IVK.

2.19 (2.19). В качестве ненапрягаемой арматуры железобетонных конструкций:

следует преимущественно применять:

а) стержневую арматуру класса А-III;

б) арматурную проволоку класса Вр-I (в сварных сетках и каркасах);

допускается применять:

в) стержневую арматуру классов А-II и А-I — для поперечной арматуры, а также в качестве продольной арматуры, если другие виды ненапрягаемой арматуры не могут быть использованы;

г) термомеханически упрочненную арматуру класса Ат-IVC — для продольной арматуры сварных каркасов и сеток;

д) горячекатаную арматуру классов A-IV, A-V, A-VI, а также термомеханически упрочненную классов Ат-V и Ат-VI — только для продольной рабочей арматуры вязаных каркасов и сеток.

Арматура классов A-V, Ат-V, A-VI, Ат-VI в конструкциях без предварительного напряжения может применяться как сжатая арматура, а в составе предварительно напряженных — как сжатая и растянутая арматура.

Ненапрягаемую арматуру классов А-III, Вр-I, А-II и А-I рекомендуется применять в виде сварных каркасов и сварных сеток.

2.20 (2.23). При выборе вида и марок стали для арматуры, устанавливаемой по расчету, должны учитываться температурные условия эксплуатации конструкций и характер их нагружения согласно табл. 17.

В климатических зонах с расчетной зимней температурой ниже минус 40 oС в случаях проведения строительно-монтажных работ в холодное время года несущая способность в стадии возведения конструкций с арматурой, допускаемой к применению только в отапливаемых зданиях, должна быть обеспечена исходя из расчетного сопротивления арматуры с понижающим коэффициентом 0,7 и расчетной нагрузки с коэффициентом надежности по нагрузке γf=1,0.

2.21 (2.24). Для монтажных (подъемных) петель элементов сборных железобетонных конструкций должна применяться горячекатаная арматурная сталь класса Ас-II, марки 10ГТ и класса А-I, марок ВСт3сп2 и ВСт3пс2.

В случае, если возможен монтаж конструкций при расчетной зимней температуре ниже минус 40 oС, для монтажных петель не допускается применять сталь марки ВСтЗпс2.

Нормативные и расчетные характеристики арматуры

2.22 (2.25). За нормативные сопротивления арматуры Rsn принимаются наименьшие контролируемые значения:

для стержневой арматуры, высокопрочной проволоки и арматурных канатов — предела текучести, физического или условного;

для обыкновенной арматурной проволоки — напряжения, равного 0,75 временного сопротивления разрыву.

Указанные контролируемые характеристики арматуры принимаются в соответствии с государственными стандартами или техническими условиями на арматурные стали и гарантируются с вероятностью не менее 0,95.

Нормативные сопротивления Rsn для основных видов стержневой и проволочной арматуры приведены соответственно в табл. 18 и 19.

Таблица 18(19)

Таблица 19(20)

2.23 (2.26). Расчетные сопротивления арматуры растяжению для предельных состояний первой и второй групп определяются путем деления нормативных сопротивлений на соответствующие коэффициенты надежности по арматуре γs, принимаемые по табл. 20.

Таблица 20(21)

Расчетные сопротивления арматуры растяжению (с округлением) для основных видов стержневой и проволочной арматуры при расчете конструкций по предельным состояниям первой группы приведены соответственно в табл. 21 и 22, а при расчете по предельным состояниям второй группы - в табл. 18 и 19.

2.24 (2.27). Расчетные сопротивления арматуры сжатию Rsc, используемые при расчете конструкций по предельным состояниям первой группы, при наличии сцепления арматуры с бетоном принимаются равными соответствующим расчетным сопротивлениям арматуры растяжению Rs, но не более 400 МПа, а для арматуры класса А-IIIв - Rsc=200 МПа.

Значения расчетных сопротивлений арматуры сжатию для основных видов стержневой и проволочной арматуры приведены соответственно в табл. 21 и 22.

Таблица 21 (22)

* В сварных каркасах для хомутов из арматуры класса А-III, диаметр которых менее 1/3 диаметра продольных стержней, значения Rsw принимаются равными 255 МПа (2600 кгс/см2).

Таблица 22 (23)

* Для случая применения в вязаных каркасах.

При расчете конструкций, для которых расчетное сопротивление бетона принято с учетом коэффициента условий работы γb2=0,9 (см. п. 3.1), допускается при соблюдении соответствующих конструктивных требований п. 5.39 принимать значения Rsc, МПа, равными для арматуры классов:

A-IV, Ат-IVK ...........................................................................  450

Ат-IVC, A-V, Ат-V, Ат-VCK, A-VI, Ат-VI, Ат-VIK, В-II,
Вр-II, K-7 и K-19 ......................................................................  500

При отсутствии сцепления арматуры с бетоном принимается значение Rsc=0.

2.25 (2.28). Расчетные сопротивления арматуры для предельных состоянии первой группы снижаются (или повышаются) путем умножения на соответствующие коэффициенты условий работы γsi, учитывающие опасность усталостного разрушения, неравномерное распределение напряжений в сечении, условия анкеровки, работу арматуры при напряжениях выше условного предела текучести и т.п.

Расчетные сопротивления арматуры для предельных состояний второй группы Rs,ser вводят в расчет с γs=1,0.

Расчетные сопротивления поперечной арматуры (хомутов и отогнутых стержней) Rsw снижаются по сравнению с Rs путем умножения на коэффициенты условий работы γs1 и γs2:

а) независимо от вида и класса арматуры - на коэффициент γs1=0,8, учитывающий неравномерность распределения напряжений в арматуре по длине рассматриваемого сечения;

б) для стержневой арматуры класса А-III, диаметром менее 1/3 диаметра продольных стержней и проволочной арматуры класса Вр-I в сварных каркасах — на коэффициент γs2=0,9, учитывающий возможность хрупкого разрушения сварного соединения.

Расчетные сопротивления растяжению поперечной арматуры (хомутов и отогнутых стержней) Rsw с учетом указанных выше коэффициентов условий работы приведены в табл. 21 и 22.

Расчетные сопротивления растяжению арматуры с условным пределом текучести умножаются на коэффициент условий работы γs6, учитывающий работу арматуры с напряжением выше условного предела текучести; определение этого коэффициента и порядок его использования приведены в п. 3.7.

Кроме того, расчетные сопротивления Rs и Rsw в соответствующих случаях следует умножать на коэффициенты условий работы согласно табл. 23.

Таблица 23 (24)

П р и м е ч а н и я: 1. Коэффициенты γs3 и γs4 по поз. 1 и 2 учитываются только при расчете на выносливость; для арматуры, имеющей сварные соединения, эти коэффициенты учитываются одновременно.

2. Коэффициенты γs3, γs4 и γs11 по поз. 1, 2 и 5 учитываются при определении расчетных сопротивлении арматуры Rs и Rsw, а коэффициенты γs5 и γs10 по поз. 3 и 4 - только при определении Rs.

2.26 (2.29). Длину зоны передачи напряжений lр для напрягаемой арматуры без анкеров следует определять по формуле

        ,        (18)

где ωp и λр принимаются по табл. 24.

К значению Rbp при необходимости вводятся коэффициенты условий работы бетона γbi (см. табл. 14).

Величина σtp в формуле (18) принимается равной большему из значений Rs и σsp с учетом первых потерь по поз. 1-5 табл. 4.

В элементах из мелкозернистого бетона группы Б (см. п. 2.1) и из легкого бетона при пористом мелком заполнителе (кроме классов В7,5—В12,5) значения ωp и λp увеличиваются в 1,2 раза по сравнению с приведенными в табл. 24.

Таблица 24(28)

П р и м е ч а н и е. Для элементов из легкого бетона классов В7,5-В12,5 значения ωр и λр увеличиваются в 1,4 раза по сравнению с приведенными в настоящей таблице.

Для стержневой арматуры периодического профиля всех классов величина lр принимается не менее 15d.

При мгновенной передаче усилия обжатия на бетон для стержневой арматуры периодического профиля значения ωр и λр увеличиваются в 1,25 раза. При диаметре стержней более 18 мм мгновенная передача усилий не допускается.

Начало зоны передачи напряжений при мгновенной передаче усилия обжатия на бетон для проволочной арматуры (за исключением высокопрочной проволоки класса Вр-II с внутренними анкерами по длине заделки) принимается на расстоянии 0,25 lр от торца элемента.

2.27 (2.30). Величины модуля упругости арматуры Еs принимаются по табл. 25.

Таблица 25 (29)

3. РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ
КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
ПЕРВОЙ ГРУППЫ

РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ

Общие указания

3.1. С целью учета влияния длительности действия нагрузок на прочность бетона расчет железобетонных элементов по прочности в общем случае производится:

а) на действие постоянных, длительных и кратковременных нагрузок, кроме нагрузок непродолжительного действия, суммарная длительность действия которых за период эксплуатации мала (ветровые нагрузки; крановые нагрузки; нагрузки от транспортных средств; нагрузки, возникающие при изготовлении, транспортировании и возведении, и т.п.), а также на действие особых нагрузок, вызванных деформациями просадочных, набухающих, вечномерзлых и т. п. грунтов; в этом случае расчетные сопротивления бетона сжатию и растяжению Rb и Rbt принимаются по табл. 13 при γb2=0,9;

6) на действие всех нагрузок, включая нагрузки непродолжительного действия, в этом случае расчетные сопротивления бетона Rb и Rbt принимаются по табл. 13 при γb2=1,1*.

* Если при учете особых нагрузок вводится дополнительный коэффициент условий работы согласно указаниям соответствующих нормативных документов (например, при учете сейсмических нагрузок), коэффициент γb2 принимается равным единице.

Если конструкция эксплуатируется в условиях, благоприятных для нарастания прочности бетона (под водой, во влажном грунте или при влажности окружающего воздуха выше 75 %, см. п. 1.5), расчет по случаю «а» производится при γb2=1,0.

При расчете прочности в стадии изготовления коэффициент γb2 принимается равным единице.

Условие прочности должно удовлетворяться при расчете как по случаю «а», так и по случаю «б».

При отсутствии нагрузок непродолжительного действия, а также аварийных нагрузок расчет прочности производится только по случаю «а».

При наличии нагрузок непродолжительного действия или аварийных нагрузок расчет производится только по случаю «б», если выполняется условие

               FI < 0,82 FII ,        (19)

где FI — усилие (момент MI, поперечная сила QI или продольная сила NI) от нагрузок, используемых при расчете по случаю «а»; при этом в расчете сечений, нормальных к продольной оси внецентренно нагруженных элементов, момент МI принимается относительно оси, проходящей через наиболее растянутый (или наименее сжатый) стержень арматуры;

FII — усилие от нагрузок, используемых при расчете по случаю «б».

Допускается производить расчет только по случаю «б» и при невыполнении условия (19), принимая расчетные сопротивления бетона Rb и Rbt (при γb2=1,0) с коэффициентом

       γbl=0,9 FII / FI ≤ 1,1 .        (20)

Для внецентренно сжатых элементов, рассчитываемых по недеформированной схеме, значения FI и FII можно определять без учета прогиба элемента.

Для конструкций, эксплуатируемых в условиях, благоприятных для нарастания прочности бетона, условие (19) приобретает вид FI < 0,9 FII, а коэффициент γbl следует принимать равным γbl=FII / FI.

3.2 (3.9). Расчет по прочности железобетонных элементов должен производиться для сечений, нормальных к их продольной оси, а также для наклонных к ней сечений наиболее опасного направления. При наличии крутящихся моментов следует проверить прочность пространственных сечений, ограниченных в растянутой зоне спиральной трещиной наиболее опасного из возможных направлений. Кроме того, производится расчет элементов на местное действие нагрузки (смятие бетона, в том числе под анкерами напрягаемой арматуры, продавливание, отрыв), выполняемый в соответствии с рекомендациями «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры» (М., ЦИТП Госстроя СССР, 1986).

При напрягаемой арматуре, не имеющей сцепления с бетоном, расчет элементов по прочности производится по специальным рекомендациям.

Изгибаемые элементы

РАСЧЕТ СЕЧЕНИЙ, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА

ОБЩИЕ УКАЗАНИЯ

3.3 (3.11). Расчет сечений, нормальных к продольной оси элемента, когда изгибающий момент действует в плоскости оси симметрии сечения и арматура сосредоточена у перпендикулярных указанной плоскости граней элемента, должен производиться согласно пп. 3.6—3.16 в зависимости от соотношения между значением относительной высоты сжатой зоны бетона ξ=x/h0, определяемой из соответствующих условий равновесия, и значением относительной высоты сжатой зоны бетона ξR (см. п. 3.6), при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs.

П р и м е ч а н и е. Если часть арматуры S с условным пределом текучести (см. п. 2.16) применяется без предварительного напряжения, то при расчете по вышеуказанным пунктам необходимо учесть следующее:

величина Asp заменяется на Asp1 - суммарную площадь сечения напрягаемой и ненапрягаемой арматуры S с условным пределом текучести; при этом в значении Аs учитывается только ненапрягаемая арматура с физическим пределом текучести;

предварительное напряжение σsp в арматуре с площадью сечения Asp1 принимается равным усредненному его значению σsp,m=σsp .

3.4 (3.18). Расчет изгибаемых элементов кольцевого сечения при соотношении внутреннего и наружного радиусов ≥ 0,5 с арматурой, равномерно распределенной по длине окружности (при числе продольных стержней не менее 6), должен производиться как и для внецентренно сжатых элементов согласно п. 3.49, принимая значение продольной силы N=0 и подставляя вместо Ne0 значение изгибающего момента М.

3.5. Расчет нормальных сечений, не оговоренных в пп. 33, 3.4 и 3.17, следует производить, пользуясь формулами общего случая расчета нормального сечения изгибаемого элемента согласно п. 3.18.

3.6 (3.12, 3.28). Значение определяется по формуле

        ,        (21)

где ω — характеристика сжатой зоны бетона, равная:

       ω=α - 0,008 Rb ,        (22)

здесь α — коэффициент, принимаемый равным для бетона:

       тяжелого .................... 0,85

       мелкозернистого (см. п. 2.1)

       групп:

               А...................... 0,80

               Б и В ............... 0,75

       легкого ...................... 0,80

Для тяжелого и легкого бетонов, подвергнутых автоклавной обработке, коэффициент α снижается на 0,05;

Rb - в МПа;

σsR - напряжение в арматуре растянутой зоны, МПа, принимаемое равным:

для арматуры с условным пределом текучести (см. п. 2.16)

σsR=Rs + 400 - σsp - Δσsp;

для арматуры с физическим пределом текучести (см. п. 2.16)

σsR=Rs - σsp ;

σsR - принимается при коэффициенте γsp < 1,0 (см. п. 1.18);

Δσsp - напряжение, равное:

при механическом, а также автоматизированных электротермическом и электротермомеханическом способах натяжения арматуры классов A-IV, A-V и A-VI

Δσsp=1500 ≥ 0 ,

здесь

σsp1 - определяется при коэффициенте γsp < 1,0 с учетом потерь по поз. 3-5 табл. 4;

при иных, кроме указанные выше .способах натяжения арматуры классов A-IV, A-V и A-VI, а также для арматуры классов В-II, Вр-II, К-7 и К-19 при любых способах натяжения Δσsp=0;

σsc,u - предельное напряжение в арматуре сжатой зоны, МПа, принимаемое равным:

500 - при использовании коэффициента условий работы бетона γb2=0,9 (см. п. 3.1);

400 - при использовании коэффициента γb2=1,0 или γb2=1,1.

При наличии напрягаемой и ненапрягаемой арматуры σsR определяется по напрягаемой арматуре. При напрягаемой арматуре разных классов допускается принимать наибольшее значение σsR.

Для некоторых классов арматуры значения ξR приведены в табл. 26 (для элементов из тяжелого бетона) и в табл. 27 (для элементов из легкого бетона и мелкозернистого бетона группы А).

Таблица 26

Окончание табл. 26

Обозначение, принятое в табл. 26:

σsp - предварительное напряжение при коэффициенте γsp < 1,0 (см. п. 1.18);

П р и м е ч а н и я: 1. При подборе арматуры, когда неизвестно напряжение σsp, допускается значение ξR определять при (σsp + Δσsp) / Rs=0,6.

2. Приведенные значения ξR вычислены без учета коэффициентов γbi по табл. 14.

Таблица 27

Обозначения, принятые в табл. 27:

σsp — см. табл. 26;

Δσsp — см. п. 3.6;

       .

П р и м е ч а н и я: 1. При подборе арматуры, когда неизвестно напряжение σsp, допускается значение определять при (σsp + Δσsp) / Rs=0,6.

2. Приведенные значения вычислены без учета коэффициентов γbi по табл. 14.

3.7 (3.13). Если соблюдается условие ξ < ξR, расчетное сопротивление арматуры Rs в оговоренных случаях умножается на коэффициент условий работы γs6, определяемый по формуле

       γs6=η - (η - 1) ≤ η ,        (23)

где η - коэффициент, принимаемый равным для арматуры классов:

A-IV............................................................        1,20

A-V, В-II, Вр-II, К-7 и К-19 ......................        1,15

A-VI ...........................................................        1,10

прочих .......................................................        1,00

Если ξ < 0,5ξR, можно, не пользуясь формулой (23), принимать γs6=η.

Коэффициент γs6 не следует учитывать для арматуры элементов:

рассчитываемых на действие многократно повторяющейся нагрузки;

армированных высокопрочной проволокой, расположенной вплотную (без зазоров);

эксплуатируемых в агрессивной среде;

в зоне передачи напряжений (см. п. 2.26).

При наличии сварных стыков в зоне элементов с изгибающими моментами, превышающими 0,9Мmax (где Мmax - максимальный расчетный момент), значение γs6 для арматуры классов A-IV и A-V принимается не более 1,1, а для арматуры класса A-VI - не более 1,05.

3.8 (3.14). Напрягаемая арматура, расположенная в сжатой от действия внешних сил зоне и имеющая сцепление с бетоном, вводится в расчет с напряжением σsc, равным  (σsc,u - σ'sp), но не более Rsc, где σ'sp определяется при коэффициенте γsp > 1,0, σsc,u — см. п. 3.6.

ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ

3.9 (3.15). Расчет прямоугольных сечений с арматурой, сосредоточенной у растянутой и сжатой граней элемента (черт. 5), производится в зависимости от относительной высоты сжатой зоны следующим образом:

        ;        (24)

а) при ξ1 ≤ ξR — из условия

М ≤ Rbbx (h0 - 0,5x) + Rsc A′s (h0 - a′s) + σsc A′sp (h0 - a′p) ,        (25)

где        .        (26)

Здесь коэффициент γs6 определяется по формуле

       ,        (27)

где ;

η - см. п. 3.7.

Черт. 5. Поперечное прямоугольное сечение изгибаемого
железобетонного элемента

Допускается коэффициент γs6 определять по формуле (23) п. 3.7, принимая ξ=ξ1 по формуле (24);

б) при ξ > ξR — из условия

M ≤ Rbbh02 + RscA′s (h0 - a′s) + σscA′sp (h0 - a′p) .        (28)        

В условии (28) значения αR и αm вычисляются по формулам:

       αR=ξR (1 - 0,5 ξR) ;        αm=ξ1 (1 - 0,5 ξ1)

или находятся по табл. 28; ξR - см. п. 3.6.

При напрягаемой арматуре растянутой зоны классов А-IIIв и А-III значение (αR + αm) / 2 в условии (28) заменяется на αR.

Если в растянутой зоне элемента имеется в большом количестве ненапрягаемая арматура с физическим пределом текучести (при RsAs > 0,2RsAsp — см. п. 2.16), то при напрягаемой арматуре с условным пределом текучести в условии (28) величина (αR + αm) / 2 заменяется на αR, а при напрягаемой арматуре с физическим пределом текучести значения ξR и αR определяются по ненапрягаемой арматуре. В этих случаях, если ξ > ξR, несущую способность сечения при необходимости можно несколько увеличить, произведя расчет по формулам общего случая согласно п. 3.18.

Если по формуле (26) х < 0, то прочность сечения проверяется из условия

       M ≤ (η Rs Asp + Rs As) (h0 - a's).         (29)

3.10. В целях экономичного использования растянутой арматуры изгибаемые элементы рекомендуется проектировать так, чтобы выполнялось условие ξ ≤ ξR.

3.11. Продольная арматура S при отсутствии напрягаемой арматуры в сжатой зоне подбирается следующим образом.

Вычисляется значение

                .        (30)

Если αm ≤ αR=ξR (1 — ξR / 2) (см. табл. 26 и 27), то сжатой ненапрягаемой арматуры по расчету не требуется. В этом случае площадь сечения напрягаемой арматуры в растянутой зоне при известной площади ненапрягаемой растянутой арматуры Аs (например, принятой из конструктивных соображений) определяется по формуле

                ,        (31)

где значение ζ и значение ξ, необходимое для вычисления γs6 (см. п. 3.7), определяются по табл. 28 в зависимости от αm.

Если αm > αR, то требуется увеличить сечение или повысить класс бетона, или установить сжатую ненапрягаемую арматуру согласно п. 3.12.

П р и м е ч а н и е. При ненапрягаемой арматуре с физическим пределом текучести, когда выполняется условие Rs As > 0,2 Rs Asp , значения ξR и αR определяются по ненапрягаемой арматуре.

Таблица 28

Для изгибаемых элементов прямоугольного сечения :

;

;

       αm=ξ (1 - 0,5 ξ) ;         ζ=1 - 0,5 ξ .

3.12. Требуемая площадь сечения сжатой ненапрягаемой арматуры при известной площади напрягаемой арматуры А′sp (например, принятой из условия ограничения начальных трещин) определяется по формуле

        ;        (32)

Если принятая площадь сечения сжатой ненапрягаемой арматуры близка к ее значению А's, вычисленному по формуле (32), то требуемая площадь сечения напрягаемой арматуры растянутой зоны определяется по формуле

        ,        (33)

где ξR - см. п. 3.6, а также примечание к п. 3.11.

Если принятая площадь сечения сжатой арматуры A's значительно превышает ее требуемое значение из формулы (32), то площадь сечения напрягаемой арматуры растянутой зоны определяется с учетом фактического значения А's.

В любом случае при наличии учитываемой в расчете арматуры S' требуемая площадь сечения напрягаемой арматуры растянутой зоны определяется по формуле

        ,        (34)

где ξ - определяется по табл. 28 в зависимости от значения

        ;        (35)

γs6 — см. п. 3.7, при этом должно выполняться условие ξ < ξR (см. табл. 26 и 27).

Если αm < 0, значение Аsp определяется по формуле

        ,        (36)

где η - см. п. 3.7.

ТАВРОВЫЕ И ДВУТАВРОВЫЕ СЕЧЕНИЯ

3.13 (3.16). Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и т.п.) и арматуру, сосредоточенную у растянутой и у сжатой граней элемента (черт. 6), производится в зависимости от положения границы сжатой зоны:

а) если граница сжатой зоны проходит в полке (черт. 6, а), т.е. соблюдается условие

       γs6RsAsp + RsAs ≤ Rb b′f h′f + Rsc A′s + σsc A′sp ,        (37)

где γs6 определяется по формуле (23) при ξ=h′f / h0, расчет производится как для прямоугольного сечения шириной b'f в соответствии с указаниями п. 3.9;

Черт. 6. Форма сжатой зоны в двутавровом поперечном сечении
железобетонного элемента

а - при расположении границы сжатой зоны в полке; б - то же, в ребре

б) если граница сжатой зоны проходит в ребре (черт. 6, б), т.е. условие (37) не соблюдается, то расчет производится следующим образом в зависимости от относительной высоты сжатой зоны ξ1:

;        (38)

при ξ1 ≤ ξR - из условия

M ≤ Rb bx (h0 - 0,5x) + Rb (b′f - b) h′f (h0 - 0,5h′f) + Rsc A′s (h0 - a′s) +

               + σsc A′s (h0 - a′p) ,         (39)

где .        (40)

Здесь γs6 определяется по формуле

       ,        (41)

где ;

η - см. п. 3.7;

при ξ1 > ξR — из условия

M ≤ Rb b h02 + Rb (b′f - b) h′f (h0 - 0,5h′f) + Rsc A′s (h0 - a′s) +

               + σsc A′sp (h0 - a′p) ,         (42)

при напрягаемой арматуре растянутой зоны классов А-IIIв и А-III значение в условии (42) заменяется на αR; αR и αm — см. п. 3.9 или табл. 28.

При большом количестве в растянутой зоне ненапрягаемой арматуры с физическим пределом текучести (когда RsAs > 0,2RsAsp) следует учитывать указания п. 3.9.

П р и м е ч а н и я: 1. При переменной высоте свесов полки допускается принимать значение h′f равным средней высоте свесов.

2. Ширина сжатой полки b'f, вводимая в расчет, не должна превышать значений, указанных в п. 3.16.

3.14. Требуемая площадь сечения сжатой ненапрягаемой арматуры определяется по формуле

,        (43)

где αR — определяется по формуле αR=ξR (1 - 0,5ξR);

ξR — см. п. 3.6.

При этом, если ξR ≤ h'f / h0, значение A's определяется как для прямоугольных сечений шириной b=b'f согласно п. 3.12.

3.15. Требуемая площадь сечения напрягаемой арматуры, расположенной в растянутой зоне, определяется следующим образом:

а) если граница сжатой зоны проходит в полке, т.е. соблюдается условие

М ≤ Rb b'f h'f (h0 - 0,5 h'f) + Rsc A′s (h0 - a's) + σsc A′sp (h0 - a'p) ,        (44)

площадь сечения растянутой арматуры определяется как для прямоугольного сечения шириной b′f в соответствии с указаниями пп. 3.11 и 3.12;

б) если граница сжатой зоны проходит в ребре, т.е. условие (44) не соблюдается, площадь сечения растянутой напрягаемой арматуры определяется по формуле

,        (45)

где ξ — определяется по табл. 28 в зависимости от значения

;

                       (46)

γs6 - см. п. 3.7.

При этом должно соблюдаться условие ξ ≤ ξR , где ξR — см. п. 3.6 и табл. 26 и 27, а также примечание к п. 3.11.

3.16 (3.16). Вводимая в расчет ширина сжатой полки b′f принимается из условия, что ширина свеса в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:

а) при наличии поперечных ребер или при h′f ≥ 0,1h — 1/2 расстояния в свету между продольными ребрами;

б) при отсутствии поперечных ребер или при расстояниях между ними бульших, чем расстояния между продольными ребрами, и h'f < 0,1h - 6h'f;

в) при консольных свесах полки:

при h′f ≥ 0,1h .................................................        6h′f

„    0,05h ≤ h′f  < 0,1h ....................................        3 h′f

„    h'f < 0,05h ...................        свесы не учитываются

Примеры расчета

Прямоугольные сечения

Пример 3. Дано: размеры сечения — b=300 мм, h=700 мм; а=50 мм; нагрузки непродолжительного действия отсутствуют; бетон тяжелый класса В25 (Rb=13 МПа при γb2=0,9); напрягаемая арматура класса A-IV (Rs=510 МПа), площадью сечения Аsр=1847 мм2 (3∅28); предварительное напряжение при γsp < 1: без учета потерь σsp1=500 МПа, с учетом всех потерь σsp2=400 МПа; ненапрягаемая арматура класса А-Ш (Rs=365 МПа), площадью сечения Аs=236 мм2 (3∅10); изгибающий момент М=580 кН⋅м; натяжение арматуры электротермическое автоматизированное.

Требуется проверить прочность сечения.

Р а с ч е т. h0=700 — 50=650 мм. По формуле (24) определим значение ξ1:

.

Поскольку натяжение арматуры класса A-IV электротермическое автоматизированное, определим значение Δσsp согласно п. 3.6:

Δσsp=1500 σsp1 / Rs - 1200=1500⋅500/510 - 1200=270 МПа > 0.

Из табл. 26 при γb2=0,9, классе арматуры A-IV, классе бетона В25 и при =1,31 находим ξR=0,65.

Поскольку ξ1=0,405 < ξR=0,65, расчет ведем из условия (25), определяя высоту сжатой зоны х по формуле (26).

Так как сечение прямоугольное, то коэффициент γs6 вычисляем по формуле (23) при ξ=0,405 и η=1,2:

γs6=η - (η - 1) =1,2 - 0,2 =1,15 < η=1,2.

Тогда: =300 мм ;

Rbbx(h0 - 0,5x)=13⋅300⋅300(650 - 0,5⋅300)=

=585 ⋅ 106 Н⋅мм=585 кН⋅м > М=580 кН⋅м,

т.е. прочность сечения обеспечена.

Пример 4. Дано: размеры сечения - b=300 мм, h=700 мм; a=60 мм, a′p=30 мм; бетон тяжелый класса В30 (Rb=15,5 МПа при γb2=0,9); напрягаемая арматура класса Вр-II, диаметром 5 мм (Rs=1050 МПа); ненапрягаемая арматура класса А-III (Rs=365 МПа); площадь сечения арматуры S : Аsр=1570 мм2 (80∅5) и Аs=236 мм2 (3∅10); площадь сечения арматуры S' - А'sр=392 мм2 (20∅5); предварительное напряжение с учетом всех потерь: для арматуры S при γsp < 1 — σsp=630 МПа, для арматуры S' при γsp > 1 - σ'sp=880 МПа; натяжение арматуры механическое; изгибающий момент М=650 кН⋅м.

Требуется проверить прочность сечения.

Р а с ч е т. h0=700 — 60=640 мм. Определяем напряжение в предварительно напряженной арматуре сжатой зоны σsc согласно п. 3.8.

Так как γb2=0,9, принимаем σsc,u=500 МПа (см. п. 3.6).

σsc=σsc,u - σ'sp=500 - 880=-380 МПа.

Из формулы (24) определим значение ξ1:

=0,634.

Поскольку напрягаемая арматура класса Вр-II, принимаем значение Δσsp=0 (см. п. 3.6).

Из табл. 26 при  γb2 > 0,9, классе арматуры Вр-II, классе бетона В30 и (σsp + Δσsp) / Rs=630 / 1050=0,6 находим значение ξR=0,46.

Так как ξ1=0,634 > ξR=0,46, прочность сечения проверяем из условия (28).

Из табл. 28 находим при ξ=ξ1=0,634 αm=0,433, а при ξR=0,46 αR=0,354.

Тогда 15,5⋅300⋅6402 -

- 380⋅392(640 - 30)=660⋅106 Н⋅мм=660 кH⋅м > М=650 кН⋅м,

т.е. прочность сечения обеспечена.

Пример 5. Дано: размеры сечения — b=300 мм, h=700 мм, а=a′s=50 мм; бетон тяжелый класса В25 (Rb=13 МПа при γb2=0,9); напрягаемая арматура S класса A-IV (Rs=510 МПа); ненапрягаемая арматура S' класса А-III (Rsc=365 МПа), площадью сечения A′s=804 мм2 (1∅32); изгибающий момент М=500 кН⋅м.

Требуется определить площадь сечения продольной напрягаемой арматуры.

Р а с ч е т. h0=700 — 50=650 мм. Площадь сечения продольной напрягаемой арматуры, расположенной в растянутой зоне, определяем согласно п. 3.12. По формуле (35) вычисляем значение αm:

=0,198 .

Из табл. 28 по значению αm=0,198 находим ξ=0,223. Из табл. 26 при γb2=0,9, классе арматуры A-IV, классе бетона В25, принимая, согласно примеч. 1, (σsp + Δσsp) / Rs=0,6, находим значение ξR=0,54.

Поскольку ξ=0,223 < ξR=0,54, то площадь сечения арматуры определяем по формуле (34).

Так как ξ=0,223 < 0,5 ξR=0,5⋅0,54=0,27, то, согласно п. 3.7, γs6=η=1,2.

Отсюда

=1410 мм2 .

Принимаем в сечении 3∅25 (Asp=1473 мм2).

Тавровые и двутавровые сечения

Пример 6. Дано: размеры сечения — b'f=1120 мм, h'f=30 мм, b=100 мм, h=300 мм, a=30 мм; бетон тяжелый класса В25 (Rb=13 МПа при γb2=0,9); предварительно напряженная арматура класса A-IV (Rs=510 МПа); изгибающий момент=23 кН⋅м.

Требуется определить площадь сечения арматуры.

Р а с ч е т. h0=300 - 30=270 мм. Расчет ведем, согласно указаниям п. 3.15, в предположении, что сжатой ненапрягаемой арматуры не требуется. Проверяем условие (44):

Rbb'fh'f (h0 - 0,5h′f)=13⋅1120⋅30 (270 - 0,5⋅30)=111,4 кН⋅м > M=23 кН⋅м, т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b=b′f=1120 мм согласно п. 3.11.

Определим значение αm по формуле (30):

=0,0217 .

Из табл. 26 при γb2=0,9, классе арматуры A-IV, классе бетона В25, принимая, согласно примеч. 1, (σsp + Δσsp) / Rs=0,6, находим ξR=0,54. Тогда из табл. 28 при ξR=0,54 αR=0,394.

Так как αm=0,0217 < αR=0,394, сжатой арматуры не требуется, и площадь сечения арматуры S вычисляем по формуле (31). Для этого по табл. 28 при αm=0,0217 находим ζ=0,989 и ξ=0,022.

Так как ξ=0,022 < 0,5 ξR=0,5⋅0,54=0,27, то, согласно п. 3.7, γs6=η=1,2.

Тогда при Аs=0

=140 мм2 .

Принимаем 1∅14 (Аsр=154 мм2).

Пример 7. Дано: размеры сечения — b'f=280 мм, h'f=200 мм, b=80 мм, h=900 мм, a=72 мм, a'=40 мм; бетон тяжелый класса В30 (Rb=15,5 МПа при γb2=0,9); напрягаемая арматура S класса A-IV (Rs=510 МПа), площадью сечения Аsр=2036 мм2 (8∅18); ненапрягаемая арматура S' класса А-III (Rsc=365 МПа), площадью сечения А's=226 мм2 (2∅12); предварительное напряжение арматуры при γsp < 1: без учета потерь - σsp1=380 МПа, с учетом всех потерь - γsp2=320 МПа; потери по поз. 3—5 табл. 4 отсутствуют; натяжение арматуры механическое; изгибающий момент M=790 кН⋅м.

Требуется проверить прочность сечения.

Р а с ч е т. h0=900 — 72=828 мм. Проверяем условие (37), принимая γs6=1:

Rbb'fh'f + RscA's=15,5⋅280⋅200 + 365⋅226=950 500 H < γs6 Rs Asp=1⋅510⋅2036=1 038 400 H, т.е. условие (37) не соблюдается; при γs6 > 1 это условие тем более не будет соблюдаться и, следовательно, граница сжатой зоны проходит в ребре, а прочность сечения проверяем согласно п. 3.13б.

Из формулы (38) определим значение

=0,327 .

Поскольку натяжение арматуры класса A-IV механическое, определим значение Δσsp согласно п. 3.6, принимая σsp1=380 МПа:

=-80 МПа < 0 .

Принимаем Δσsp=0.

Из табл. 26 при γb2=0,9, классе арматуры A-IV, классе бетона В30 и (σsp + Δσsp) / Rs=320 / 510=0,627 находим ξR=0,52.

Поскольку ξ1=0,327 < ξR=0,52, расчет ведем из условия (39) с учетом коэффициента γs6, определяемого по формуле (41):

=0,684 ;

η=1,2 (см. п. 3.7);

=

=1,082 < η=1,2.

Высота сжатой зоны равна:

340 мм.

Тогда Rbbx(h0 - 0,5x) + Rb (b'f - b)h′f(h0 - 0,5h′f)+ RscA′s (h0 - а's)=

=15,5⋅80⋅340(828 - 0,5⋅340) + 15,5⋅200⋅200(828 - 0,5⋅200) +

+ 365⋅226(828 - 40)=795⋅106 Н⋅мм=795 кН⋅м > М=790 кН⋅м,

т.е. прочность сечения обеспечена.

Пример 8. Дано: балка покрытия с размерами сечения - b'f=280 мм, h'f =200 мм, b=80 мм, h=900 мм, a=90 мм, a′s=40 мм; бетон тяжелый класса В35; напрягаемая арматура S из канатов класса К-7, диаметром 15 мм (Rs=1080 МПа); ненапрягаемая арматура S' класса A-III (Rsc=365 МПа), площадью сечения А′s=226 мм2 (2∅12); изгибающие моменты: без учета нагрузки от подвесного транспорта MI=740 кН⋅м, с учетом нагрузки от подвесного транспорта MII=1000 кН⋅м.

Требуется определить площадь сечения напрягаемой арматуры S.

Р а с ч е т. Проверяем условие (19) :

0,82MII=0,82⋅1000=820 кН⋅м > MI=740 кН⋅м, т.е. расчет ведем только по случаю «б» — на действие момента М=МII=1000 кН⋅м, принимая Rb=21,5 МПа при γb2=1,1;

h0=h - a=900 - 90=810 мм.

Проверяем условие (44):

Rb b'f h'f - 0,5h'f) + Rsc A′s (h0 - a′s )=21,5⋅280⋅200(810 - 0,5⋅200) +

+ 365⋅226(810 - 40)=918⋅106 Н⋅мм=918 кН⋅м < M=1000 кН⋅м,

т.е. граница сжатой зоны проходит в ребре, и поэтому требуемую арматуру определяем согласно п. 3.15б.

По формуле (46) определяем значение αm:

=0,29.

Из табл. 28 при αm=0,29 находим ξ=0,35.

Из табл. 26 при γb2=1,1, классе арматуры К-7, классе бетона В35 и (σsp + Δσsp) / Rs=0,6 находим ξR=0,38.

Так как ξ=0,35 < ξR=0,38, то сжатой арматуры поставлено достаточно, и площадь сечения арматуры S вычисляем по формуле (45).

Для этого, согласно п. 3.7, определим коэффициент γs6.

Для арматуры класса К-7 η=1,15.

=1,024 < η=1,15.

Тогда

=1293 мм2.

Принимаем 10∅15 (Аsp=1416 мм2).

ЭЛЕМЕНТЫ, РАБОТАЮЩИЕ НА КОСОЙ ИЗГИБ

3.17. Расчет прямоугольных, тавровых, двутавровых и Г-образных сечений элементов, работающих на косой изгиб, допускается производить, принимая форму сжатой зоны по черт. 7; при этом должно удовлетворяться условие

       Мх ≤ Rb [Soν,x +Aweb (h0 - x1/3)] Rsc Ssx + σsc Sspx ,        (47)

где Мх — составляющая изгибающего момента в плоскости оси х (за оси х и у принимаются две взаимно перпендикулярные оси, проходящие через точку приложения равнодействующей усилий в растянутой арматуре, параллельно сторонам сечения; для сечения с полкой ось х принимается параллельно плоскости ребра);

Aweb=Ab - Aoν ;                (48)

Ab — площадь сжатой зоны бетона, равная:

       ;        (49)

Aoν — площадь сечения наиболее сжатого свеса полки;

x1 — размер сжатой зоны бетона по наиболее сжатой стороне сечения, определяемый по формуле

       x1=-t + ;        (50)

здесь        ;        (51)

Soν,x — статический момент площади Аoν в плоскости оси х относительно оси у;

Soν,y — то же, в плоскости оси у относительно оси x;

b0 — расстояние от равнодействующей усилий в растянутой арматуре до наиболее сжатой боковой стороны сечения (грани ребра);

β — угол наклона плоскости действия изгибающего момента к оси x, т.e. ctg β=Mx / My;

Ssx, Sspx — статические моменты площади сечения соответственно ненапрягаемой и напрягаемой арматуры относительно оси у.

Черт. 7. Форма сжатой зоны в поперечном сечении железобетонного элемента, работающего на косой изгиб

а — таврового сечения; б — прямоугольного сечения; 1-1 — плоскость действия изгибающего момента; 2 — точка приложения
равнодействующей усилий в растянутой арматуре

При расчете прямоугольных сечений значения Aoν, Soν,x и Soν,y в формулах (47), (48) и (51) принимаются равными нулю.

Если Ab < Аoν или если х < 0,2h′f, расчет производится как для прямоугольного сечения шириной b=b'f.

Если выполняется условие

                ,        (52)

где boν — ширина наименее сжатого свеса полки,

расчет производится без учета косого изгиба, т.е. по формулам пп. 3.9 и 3.13 на действие момента М=Мx; при этом следует проверить условие (55), принимая х1, как при косом изгибе.

Приведенную методику расчета следует применять, если относительная высота сжатой зоны, измеренная по нормали к границе сжатой зоны и определяемая по формуле (53), меньше или равна ξR (см. п. 3.6):

        ,        (53)

где boν — ширина наиболее сжатого свеса;

θ — угол наклона прямой, ограничивающей сжатую зону, к оси у, значение tg θ определяется по формуле

       tg θ=x12 / (2Aweb),        (54)

x1 — для определения ξ1 вычисляется по формуле (50) при γs6=1,0.

Для проверки условия (47) коэффициент γs6 в формуле (49) определяется, согласно п. 3.7, при значении ξ, принимаемом равным:

при отсутствии в сжатой зоне полки ξ=ξ1 ;

при наличии в сжатой зоне полки ξ=(ξ1 + ξR) / 2.

Если выполняется условие

               ξ1 > ξR ,        (55)

следует произвести повторный расчет с заменой для напрягаемой арматуры в формуле (49) значения γs6 Rs напряжением σs, равным:

для арматуры с условным пределом текучести (см. п. 2.16):

при ξ ≤ ξel (где ξel — см. п. 3.18 или табл. 31)

        ;        (56)

при ξ > ξel

        ,        (57)

где β - см. п. 3.18;

σsc,u , ω, σsp — см. п. 3.6; значение ω, а также выражение можно находить по табл. 31;

для арматуры с физическим пределом текучести — по формуле (57).

При этом ненапрягаемую арматуру с физическим пределом текучести, если площадь ее сечения не превышает 0,2Asp, допускается учитывать в формуле (49) с полным расчетным сопротивлением. При большей площади указанной ненапрягаемой арматуры, если ξ > ξR (где ξR определено для этой арматуры), в формуле (49) значение Rs для ненапрягаемой арматуры заменяется на напряжение σs, определяемое по формуле (57).

Если выполняются условия (58) и (59), то расчет на косой изгиб производится по формулам общего случая расчета нормального сечения согласно п. 3.18:

для прямоугольных и тавровых сечений с полкой в сжатой зоне

               x1 > h ;        (58)

для двутавровых и тавровых сечений с полкой в растянутой зоне

       x1 > h - hf - boν,t tg θ ,        (59)

где hf, boν,t — высота и ширина наименее растянутого свеса полки (черт.8).

Черт. 8. Двутавровое сечение со сжатой зоной, заходящей
в наименее растянутый свес полки

1-1— плоскость действия изгибающего момента

При использовании формул настоящего пункта за растянутую арматуру площадью Аsp и Аs рекомендуется принимать арматуру, располагаемую вблизи растянутой грани, параллельной оси у, а за сжатую арматуру площадью А'sp и A's - арматуру, располагаемую вблизи сжатой грани, параллельной оси у, но по одну наиболее сжатую сторону от оси х (см. черт. 7).

Если арматура распределена по сечению, что не позволяет до расчета определить площади и центры тяжести сечений арматуры S и S', расчет также производится по формулам общего случая согласно п. 3.18.

При наличии ненапрягаемой арматуры с условным пределом текучести учитывается примечание к п. 3.3.

Примеры расчета

Пример 9. Дано: железобетонный прогон кровли с уклоном 1:4; размеры сечения по черт. 9; класс бетона В25 (Rb=13 МПа при γb2=0,9); арматура S класса A-IV (Rs=510 МПа) площадью сечению Аsp=314,2 мм2 (1∅20); арматура S' класса A-III (Rsc=365 МПа) площадью сечения А′s=226 мм2 (2∅12); предварительное напряжение арматуры при γsp < 1 с учетом всех потерь σsp=306 МПа; натяжение арматуры - электротермическое.

Требуется определить предельный изгибающий момент в вертикальной плоскости.

Р а с ч е т    ведем без учета стержня, расположенного в наименее сжатом свесе. Из черт. 9 имеем:

h0=h - а=300 - 30=270 мм; b0==55 мм;

boν=b′oν=55 мм; h′f=60 мм.

Черт. 9. К примеру расчета 9

1-1 — плоскость действия изгибающего момента

Определяем площадь сжатой зоны бетона по формуле (49), учитывая один стержень арматуры S′, т.е. А′s=113 мм2 (1∅12), и принимая γs6=1:

=9154 мм2 .

Площадь сечения наиболее сжатого свеса и ее статические моменты относительно осей х и у соответственно равны:

Аоν=b'oν h'f=55⋅60=3300 мм2;

Soν,y=Aоν (b0 + 0,5b′oν)=3300 (55 + 0,5⋅55)=272 000 мм3 ;

Soν,x=Aоν (h0 - 0,5h'f)=3300 (270 - 0,5⋅60)=792 000 мм3

Так как Аb >Аoν, далее расчет производим как для таврового сечения:

Aweb=Ab - Aoν=9154 - 3300=5854 мм2.

Определяем размер сжатой зоны х1 по формуле (50), принимая ctg β=4:

=0,9 мм ;

х1=-t + =215,7 мм .

Проверим условие (52):

=53,2 мм < х1=215,7 мм,

следовательно, расчет продолжаем по формулам косого изгиба.

Определим значение ξ1 по формуле (53), вычислив:

3,97 ;

=0,614 .

Поскольку натяжение арматуры электротермическое неавтоматизированное, принимаем, согласно п. 3.6, Δσsp=0.

Из табл. 26 и 31 при γb2=0,9, классе арматуры A-IV, классе бетона В25 и при (σsp + Δσsp) / Rs=306/510=0,6 находим ξR=0,54 и ξel=0,7.

Поскольку выполняется условие (55):

ξ1=0,614 > ξR=0,54,

расчет повторяем, заменяя в формуле (49) значение Rs на напряжение σs, определенное по формуле (56).

Согласно п. 3.18, β=0,8;

=486 МПа;

=8574 мм2 ;

Aweb=8574 - 3300=5274 мм2 ;

9 мм ;

х1=-9 + =197 мм .

Определяем предельный изгибающий момент в плоскости оси х из условия (47):

Мх,u=Rb[Soν,x +Aweb (h0 - х1/3)] + Rsc Ssx=13[792000+5274(270-197/3)] +

+ 365⋅113(270 - 20)=34,6⋅106 Н⋅мм=34,6 кН⋅м.

Предельный изгибающий момент в вертикальной плоскости равен:

=35,6 кН⋅м .

ОБЩИЙ СЛУЧАЙ РАСЧЕТА НОРМАЛЬНЫХ СЕЧЕНИЙ
ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ (ПРИ ЛЮБЫХ ФОРМАХ
СЕЧЕНИЯ, НАПРАВЛЕНИЯХ ДЕЙСТВИЯ ВНЕШНЕГО
МОМЕНТА И ЛЮБОМ АРМИРОВАНИИ)

3.18 (3.28). Расчет нормальных сечений изгибаемого элемента в общем случае (черт. 10) выполняется из условия

       M ≤ Rb Sb - Σσsi Ssi ,        (60)

где М — проекция момента внешних сил на плоскость, перпендикулярную прямой, ограничивающей сжатую зону сечения;

Sb — статический момент площади сжатой зоны бетона относительно оси, параллельной прямой, ограничивающей сжатую зону и проходящей через центр тяжести сечения наиболее растянутого стержня;

Ssi — статический момент площади сечения i-го стержня продольной арматуры относительно указанной оси;

σsi — напряжение в i-м стержне продольной арматуры.

Черт. 10. Схема усилий и эпюра напряжений в сечении,
нормальном к продольной оси железобетонного элемента,
в общем случае расчета по прочности

1-1 - плоскость, параллельная плоскости действия изгибающего момента; 1 - точка приложения равнодействующих усилий в сжатой арматуре и в бетоне сжатой зоны; 2 - точка приложения равнодействующей усилий в растянутой арматуре

Высота сжатой зоны х и напряжения σsi определяются из совместного решения уравнений:

               Rb Ab=Σσsi Asi ,          (61)

при ξi ≤ ξRi

        ,          (62)

где η - см. п. 3.7;

при ξel,i ≥ ξi > ξRi

        ;          (63)

при ξi > ξel,i

       .         (64)

Для продольной арматуры с физическим пределом текучести (см. п. 2.16) при ξi > ξRi используется только уравнение (64).

В формулах (61) - (64):

Ab — площадь сжатой зоны бетона;

Asi — площадь сечения i-го стержня продольной арматуры;

ξi —относительная высота сжатой зоны, равная:

,

где h0i - расстояние от оси, проходящей через центр тяжести сечения рассматриваемого i-го стержня арматуры и параллельной прямой, ограничивающей сжатую зону, до наиболее удаленной точки сжатой зоны сечения (см. черт. 10);

ξRi, ξel,i - относительная высота сжатой зоны, отвечающая достижению в рассматриваемом стержне напряжений, соответственно равных Rsi и βRsi, значение ξRi определяют по формуле (21) п. 3.6, значение ξel,i — также по формуле (21), принимая

               σsR=βRsi - σspi ,        (65)

здесь β - коэффициент, принимаемый равным:

при механическом, а также автоматизированных электротермическом и электротермомеханическом способах натяжения арматуры классов A-IV, A-V, A-VI

        ,        (66)

где σsp1i - определяется при γsp < 1,0 (см. п. 1.18) с учетом потерь по поз. 3—5 табл. 4;

σsc,u, ω - см. п. 3.6;

при иных, кроме указанных выше, способах натяжения арматуры классов A-IV, A-V и A-VI, а также для арматуры классов В-II, Вр-II, К-7 и К-19 при любых способах натяжения β=0,8.

Напряжения σsi, определенные по формуле (64), вводятся в расчет со своими знаками; при этом напряжения со знаком «плюс» означают растягивающие напряжения, а напряжения со знаком «минус» — сжимающие. Напряжения σsi принимаются не менее -Rsc (максимальное сжимающее напряжение) и не менее σsp — σsc,u .

Напряжение σspi в формуле (64) определяется при коэффициенте γsp < 1,0, если рассматриваемый стержень расположен в растянутой зоне, и γsp > 1,0, если стержень расположен в сжатой зоне.

Для определения положения границы сжатой зоны при косом изгибе (т.е. когда плоскость действия момента не перпендикулярна прямой, ограничивающей сжатую зону) кроме использования формул (61)-(64) требуется соблюдение условия параллельности плоскости действия моментов внешних и внутренних сил.

Если в сечении можно выявить характерную ось (например, ось симметрии или ось ребра Г-образного сечения), то при косом изгибе расчет рекомендуется производить в следующем порядке.

1. Провести две оси х и у соответственно параллельно и перпендикулярно указанной характерной оси через центр тяжести сечения наиболее растянутого стержня.

2. Подобрать последовательными приближениями положение прямой, ограничивающей сжатую зону, при постоянном угле ее наклона θ так, чтобы удовлетворялось равенство (61) после подстановки в него значений σsi, определенных по формулам (62)-(64); при этом угол θ в первом приближении принять равным углу наклона нулевой линии, определенному как для упругого материала.

3. Определить моменты внутренних сил в плоскости осей х и у соответственно Mx,u и My,u.

4. Если оба момента оказываются больше или меньше соответствующих составляющих внешнего момента (Мx и My), то прочность сечения считается соответственно обеспеченной или необеспеченной.

5. Если один из этих моментов (например, Му,u) меньше соответствующей составляющей внешнего момента (My), а другой момент больше составляющей внешнего момента (т.е. Мx,u > Мs), то следует задаться другим углом θ (бульшим, чем ранее принятый) и снова выполнить аналогичный расчет.

Примеры расчета

Пример 10. Дано: железобетонная шпала с размерами расчетного поперечного сечения по оси рельса - по черт. 11; бетон тяжелый класса В40 (Rb=24 МПа при γb2=1,1); арматура из проволоки класса Вр-II, диаметром 3 мм (Rs=1215 МПа); предварительное напряжение арматуры при γsp < 1 σsp=975 МПа; изгибающий момент в расчетном сечении М=26 кН⋅м.

Требуется проверить шпалу на прочность.

Черт. 11. К примеру расчета 10

Р а с ч е т. В связи с распределенным характером расположения арматуры по сечению расчет производим по общему случаю согласно п. 3.18.

По формуле (21) п. 3.6 определяем значения ξR и ξel. Для этого вычислим ω=0,85 - 0,008 Rb=0,85 - 0,008⋅24=0,658. Поскольку арматура проволочная, принимаем Δσsp=0 и β=0,8, σsc,u=400 МПа (так как γb2=1,1).

Значение σsR равно:

при вычислении ξR

σsR=Rs + 400 - σsp=1215 + 400 - 975=640 МПа;

при вычислении ξel

σsR=βRs - σsp=0,8 ⋅ 1215 - 975=-3 МПа.

Отсюда имеем:

.

Задавшись высотой сжатой зоны х, определим напряжение σsi каждого горизонтального ряда спаренных проволок по формулам (62)-(64) :

при ξi ≤ ξR

;

при ξel ≥ ξi > ξR

= 1640 - 1010 ξ ;

при ξi > ξel

.

Затем определим сумму усилий во всех рядах проволок ΣσsiAsi, где Asi принимается равной площади сечения арматуры в одном i-м ряду, параллельном нейтральной оси.

В первом приближении значение х определим из уравнения (61), принимая среднее напряжение в арматуре равным 0,9Rs = 0,9⋅1215 = 1093 МПа;

ΣAsi = 367 мм2 (52∅3),

отсюда        = 16700 мм2 .

Поскольку сжатая зона имеет трапециевидную форму, высоту сжатой зоны х определим из уравнения (см. черт. 11)

откуда =

= 87,5 мм.

Вычисления приводим в табличной форме (табл. 28а).

Таблица 28а

Окончание табл. 28а

Исходя из вычисленного значения ΣσsiAsi (с учетом х = 87,5 мм), вновь определяем:

12900 мм2 ;

х = -313 + 70 мм < 87,5 мм ,

т.е. значение х в первом приближении принято завышенным.

Во втором приближении значением принимаем равным 76 мм и производим аналогичный расчет (см. табл. 28а) :

14450 мм2 ;

х=-313 + 78 мм ≈ 76 мм ,

т.е. значение х=76 мм принято правильно.

Определим статический момент сжатой зоны бетона в виде трапеции относительно нижнего ряда проволок Sb. Ширина сечения по границе сжатой зоны равна:

b2=167 + 2⋅0,267⋅76=208 мм; b1=167 мм.

Тогда        Sb=

1,65 ⋅ 106 мм3.

Момент усилия в арматуре относительно центра тяжести нижнего ряда проволок определим по формуле

Σ σsi Ssi=Σ σsi Asi (h01 - hoi) .

Вычисление Σ σsi Ssi  приведено в табл. 28а.

Проверяем условие (60):

RbSb - Σ σsi Ssi=24⋅1,65⋅106 - 11,9⋅106=27,7⋅106 Н⋅мм=

=27,7 кН⋅м > М=26 кН⋅м,

т.е. прочность шпалы обеспечена.

РАСЧЕТ СЕЧЕНИЙ, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА

3.19 (3.29). Расчет элементов по наклонным сечениям должен производиться для обеспечения прочности:

на действие поперечной силы по наклонной полосе между наклонными трещинами - согласно п. 3.21;

на действие поперечной силы по наклонной трещине для элементов с поперечной арматурой — согласно пп. 3.22—3.29, для элементов без поперечной арматуры — согласно п. 3.30;

на действие изгибающего момента по наклонной трещине — согласно пп. 3.31—3.34.

Расчет элементов с поперечной арматурой на действие поперечной силы, согласно пп. 3.22—3.29, не производится, если выполняются условия прочности п. 3.30. При соблюдении этих условий поперечная арматура определяется конструктивными требованиями (см. пп. 5.41 и 5.42).

П р и м е ч а н и е. В настоящем Пособии под поперечной арматурой имеются в виду хомуты и отогнутые стержни (отгибы). Термин «хомуты» включает в себя поперечные стержни сварных каркасов и хомуты вязаных каркасов.

3.20. Расстояния между хомутами s, между опорой и концом отгиба, ближайшего к опоре, s1, а также между концом предыдущего и началом последующего отгиба s2 (черт. 12) должны быть не более величины

        ,        (67)

где φn — см. п. 3.22;

φb4 — см. табл. 29.

Кроме того, эти расстояния должны удовлетворять конструктивным требованиям пп. 5.42 и 5.44.

Черт. 12. Расстояния между хомутами и отгибами

РАСЧЕТ НА ДЕЙСТВИЕ ПОПЕРЕЧНОЙ СИЛЫ
ПО НАКЛОННОЙ СЖАТОЙ ПОЛОСЕ

3.21 (3.30). Расчет элементов на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами должен производиться из условия

       Q ≤ 0,3 φw1 φb1 Rb b h0 ,        (68)

где Q - поперечная сила, принимаемая на расстоянии от опоры не менее h0;

φw1 — коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, и определяемый по формуле

               φw1=1 + 5αμw ,        (69)

но не более 1,3;

;

φb1 — коэффициент, определяемый по формуле

               φb1=1 - β Rb ,        (70)

β — коэффициент, принимаемый равным для бетона:

тяжелого и мелкозернистого ....... 0,01

легкого ......................................... 0,02

Rb — в МПа.

При линейном изменении ширины b по высоте в расчет [в формулы (67), (68) и последующие] вводится ширина сечения на уровне середины высоты сечения без учета полок.

РАСЧЕТ НА ДЕЙСТВИЕ ПОПЕРЕЧНОЙ СИЛЫ
ПО НАКЛОННОЙ ТРЕЩИНЕ

Элементы постоянной высоты, армированные хомутами
без отгибов

3.22. Проверка прочности наклонного сечения на действие поперечной силы по наклонной трещине (черт. 13) производится из условия

               Q ≤ Qb + qsw c0 ,        (71)

где Q — поперечная сила от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем через наиболее удаленный от опоры конец наклонного сечения; при нагрузке, приложенной к нижней грани элемента или в пределах высоты его сечения, также допускается значение Q принимать в наиболее удаленном от опоры конце наклонного сечения, если хомуты, установленные на действие отрыва1, не учитываются в данном расчете; при этом следует учитывать возможность отсутствия временной нагрузки на участке в пределах наклонного сечения;

1 Расчет на отрыв производится согласно п. 3.97 «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры» (М., ЦИТП Госстроя СССР, 1986).

Черт. 13. Схема усилий в наклонном сечении элемента, армированного хомутами без отгибов, при расчете его на действие поперечной силы

Qb — поперечное усилие, воспринимаемое бетоном и равное:

               .        (72)

Здесь        Mb=φb2 (1 + φf + φn) Rbt b h02 ;        (73)

φb2 — коэффициент, учитывающий вид бетона и определяемый по табл. 29;

φf — коэффициент, учитывающий влияние сжатых полок и определяемый по формуле

       , но не более 0,5 ;        (74)

при этом величина (b′f - b) принимается не более 3h′f,

учет полок производится, если поперечная арматура в ребре заанкерена в полке, где расположена поперечная арматура, соединяющая свесы полки с ребром;

φn — коэффициент, учитывающий влияние предварительного напряжения арматуры растянутой зоны и определяемый по формуле

                ,        (75)

где P=σsp Asp - σs As; суммарный коэффициент 1 + φf + φn принимается не более 1,5;

с - длина проекции наклонного сечения на продольную ось элемента.

Таблица 29

Значение Qb принимается не менее

Qb,min=φb3 (1 + φf + φn) Rbt b h0 (φb3 - см. табл. 29);

qsw — усилие в хомутах на единицу длины элемента в пределах наклонного сечения, определяемое по формуле

               qsw=;        (76)

c0 — длина проекции наклонной трещины на продольную ось элемента, принимаемая равной:

               c0= ,        (77)

но не более с и не более 2h0, а также не менее h0, если с > h0.

При этом для хомутов, устанавливаемых по расчету (т.е. когда не выполняются условия п. 3.30), должно удовлетворяться условие

               qsw ≥ .        (78)

Разрешается не выполнять условие (78), если в формуле (73) учитывать такое уменьшенное значение Rbt b, при котором условие (78) превращается в равенство, т.е. если принимать Мb=2 h02 qsw ; в этом случае всегда с0=2h0, но не более с.

При проверке условия (71)в общем случае задаются рядом наклонных сечений при различных значениях с, не превышающих расстояния от опоры до сечения с максимальным изгибающим моментом, а также значения (φb2 / φb3) h0 .

При действии на элемент сосредоточенных сил значения с принимаются равными расстояниям от опоры до точек приложения этих сил (черт. 14).

Черт. 14. Расположение невыгоднейших наклонных сечений при
действии на элемент сосредоточенных и прерывистых нагрузок

1-1 и 2-2 - наклонные сечения, проверяемые на действие соответственно сил Q1 и Q2

При расчете элемента на действие равномерно распределенной нагрузки q значение с принимается равным , а если q1 > 0,56qsw,  следует также принимать с=, где значение q1 определяется следующим образом:

а) если равномерно распределенная нагрузка q всегда сплошная — q1=q,

б) если нагрузка q включает в себя временную эквивалентную равномерно распределенную нагрузку ν (т.е. временная нагрузка несплошная, а эпюра моментов М от принятой в расчете нагрузки v всегда огибает эпюру М от любой фактической временной нагрузки) — q1=g + ν/2 (g — постоянная сплошная нагрузка).

При этом значение Q принимается равным Qmax - q1c (Qmax — поперечная сила в опорном сечении).

3.23. Определение требуемой интенсивности хомутов, выражаемой через qfw (см. п. 3.22), производится следующим образом:

а) при действии на элемент сосредоточенных сил, располагаемых на расстояниях сi от опоры, для каждого наклонного сечения с длиной проекции ci, не превышающей расстояния до сечения с максимальным изгибающим моментом, значение qsw определяется в зависимости от коэффициента xi=(где Qbi — см. п. 3.22) по одной из следующих формул:

при xi < x0i=        qsw(i)=;        (79)

при x0i ≤ xi ≤                  qsw(i)=;        (80)

при                   qsw(i)= ;        (81)

при xi >                          qsw(i)=        (82)

(здесь h0 принимается не более сi).

Окончательно принимается наибольшее значение qsw(i).

В формулах (79) - (82) :

Qi - поперечная сила в нормальном сечении, расположенном на расстоянии сi от опоры;

c0 - принимается равным сi, но не более 2h0;

б) при действии на элемент только равномерно распределенной нагрузки q требуемая интенсивность хомутов определяется по формулам:

при Qmax ≤                    ;        (83)

при            ;        (84)

в обоих случаях qsw принимается не менее ;

при Qmax >             qsw = .         (85)

В случае, если полученное значение qsw не удовлетворяет условию (78), следует снова вычислить qsw по формуле

,

где Qb1 = ;

Qmax - поперечная сила в опорном сечении;

Mb, q1, φb2, φb3 - см. п. 3.22.

3.24. При уменьшении интенсивности хомутов от опоры к пролету с qsw1 на qsw2 (например, увеличением шага хомутов) следует проверить условие (71) при значениях с, превышающих l1 - длину участка элемента с интенсивностью хомутов qsw1 (черт. 15). При этом выражение qswc0 заменяется:

при c - l1 < c01                на qsw1 c01 - (qsw1 - qsw2) (c - l1) ;

при c02 > c - l1 ≥ c01        на qsw2 (c - l1) ;

при c - l1 ≥ c02                на qsw2 c02 ,

где значения c01 и c02 определяются по формуле (77) при qsw, соответственно равном qsw1 и qsw2.

Черт. 15. Изменение интенсивности хомутов в пределах наклонного
сечения

При действии на элемент равномерно распределенной нагрузки длина участка l1 с интенсивностью qsw1 определяется следующим образом:

при q1 > qsw1 - qsw2         ,

где , но не более ;

при q1 ≤ qsw1 - qsw2        .

Здесь q1 — см. п. 3.22.

Если для интенсивности qыц2 не выполняется условие (78), длина l1 вычисляется при скорректированных значениях Мb = 2h02 qsw2 φb2 / φb3 и Qb,min = 2 h0 qsw2 ; при этом выражение (Qb,min + qsw2 c01) принимается не менее нескорректированного значения Qb,min.

Элементы постоянной высоты, армированные отгибами

3.25. Проверка прочности наклонного сечения на действие поперечной силы для элемента с отгибами производится из условия (71) п. 3.22 с добавлением к правой части условия (71) значения

       Qs,inc = As,inc Rsw sin θ ,        (86)

где As,inc - площадь сечения отгибов, пересекающих опасную наклонную трещину с длиной проекции c0;

θ - угол наклона отгибов к продольной оси элемента.

Значение c0 принимается равным длине участка элемента в пределах рассматриваемого наклонного сечения, для которого выражение qswc0 + Qs,inc + Мb / c0 принимает минимальное значение. Для этого рассматриваются участки от конца наклонного сечения или от конца отгиба в пределах длины с до начала отгиба, более близкого к опоре или до опоры (черт. 16), при этом длина участка принимается не более значения c0, определяемого по формуле (77).

Черт. 16. К определению наиболее опасной наклонной трещины
для элементов с отгибами

1, 2, 3 — возможные наклонные трещины; 4-4 — рассматриваемое
наклонное сечение

Наиболее опасная наклонная трещина на черт. 16 соответствует минимальному значению из следующих выражений:

qsw c01 + Rsw As,inc1 sin θ1 + Mb / c01 ;

qsw c0 + Rsw As,inc2 sin θ2 + Mb / c0 [здесь с0 - см. формулу (77)];

qsw c03 + Mb / c03 .

Значения с принимаются равными расстояниям от опоры до конца отгибов, а также до мест приложения сосредоточенных сил (см. черт. 16), кроме того, следует проверить наклонные сечения, заканчивающиеся на расстоянии с0, определяемом по формуле (77), от начала последнего и предпоследнего отгибов.

Элементы переменной высоты с поперечным армированием

3.26 (3.33). Расчет элементов с наклонными сжатыми гранями на действие поперечной силы производится согласно пп. 3.22, 3.24 и 3.25 с учетом указаний пп. 3.27 и 3.28, принимая в качестве рабочей высоты наибольшее значение h0 в пределах рассматриваемого наклонного сечения (черт. 17, а, в).

Расчет элементов с наклонными растянутыми гранями на действие поперечной силы допускается производить согласно пп. 3.22, 3.24 и 3.25, также принимая в качестве рабочей высоты наибольшее значение h0 в пределах наклонного сечения в растянутой зоне (черт. 17, б).

Черт. 17. Наклонные сечения элементов с переменной высотой сечения

а - балка с наклонной сжатой гранью; б - балка с наклонной растянутой гранью; в - консоль с наклонной сжатой гранью

3.27. Для балок без отгибов с высотой, равномерно увеличивающейся от опоры к пролету (черт. 17, а, б), рассчитываемых на действие равномерно распределенной нагрузки q, наклонное сечение проверяется из условия (71) п. 3.22 при невыгоднейшем значении с, определяемом следующим образом:

если выполняется условие

       q1 < 0,56 qsw - 2,5 ,        (87)

значение с вычисляется по формуле

        ;        (88)

если условие (87) не выполняется, значение с вычисляется по формуле

               (89)

       (при этом c0 = с),

а также, если qsw < Mbs / (4 h02s),  - по формуле

               (90)

       (при этом c0 = 2 h0),

где qinc = φb2 (1 + φfs + φns) Rbt b tg2β ;

Mbs - величина Mb, определяемая по формуле (73) как для опорного сечения балки с рабочей высотой h0 s, без учета приопорного уширения;

β - угол между сжатой и растянутой гранями балки;

φfs, φns - коэффициенты φf и φn при h0 = h0s.

Рабочая высота h0 при этом принимается равной h0 = h0s + сtgβ.

При уменьшении интенсивности хомутов от опоры к пролету следует проверить прочность наклонных сечений, заходящих в участок с меньшей интенсивностью хомутов, учитывая указания п. 3.24.

Участки балки с постоянным характером увеличения рабочей высоты h0 не должны быть менее принятого значения с.

При действии на балку сосредоточенных сил проверяются наклонные сечения при значениях с, принимаемых согласно п. 3.22, а также определяемых, если tg β > 0,1, по формуле (89) при q1 = 0.

3.28. Для консолей без отгибов с высотой, равномерно увеличивающейся от свободного конца к опоре (черт. 17, в), в общем случае следует проверить условие (71), задаваясь наклонными сечениями со значениями с, определяемыми по формуле (89) при q1 = 0 и принимаемыми не более расстояния от начала наклонного сечения в растянутой зоне до опоры. При этом за h0s и Q необходимо принимать соответственно рабочую высоту и поперечную силу в начале наклонного сечения в растянутой зоне. Кроме того, следует проверить наклонные сечения, проведенные до опоры, если при этом с0 < с.

При действии на консоль сосредоточенных или прерывистых нагрузок начала наклонных сечений располагают в растянутой зоне нормальных сечений, проходящих через концы площадок опирания этих нагрузок (черт. 17, в).

При действии равномерно распределенной нагрузки или нагрузки, линейно увеличивающейся к опоре, консоль рассчитывают так же, как элемент с постоянной высотой сечения, согласно п. 3.22, принимая рабочую высоту h0 в опорном сечении.

Элементы с поперечным армированием при косом изгибе

3.29. Расчет по поперечной силе элементов прямоугольного сечения, подвергающихся косому изгибу, производится из условия

        ,        (91)

где Qx, Qy - составляющие поперечной силы, действующие соответственно в плоскости симметрии х и в нормальной к ней плоскости у в наиболее удаленном от опоры конце наклонного сечения;

Qbw(х), Qbw(y) — предельные поперечные силы, которые могут быть восприняты наклонным сечением при действии их соответственно только в плоскости х и только в плоскости у, принимаемые равными правой части условия (71).

При действии на элемент равномерно распределенной нагрузки допускается определять значения с, согласно п. 3.22, независимо для каждой плоскости х и у.

П р и м е ч а н и е. Отгибы при расчете на поперечную силу при косом изгибе не учитываются.

Элементы без поперечной арматуры

3.30 (3.32). Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий:

       a) Qmax ≤ 2,5 Rbt b h0 ,        (92)

где Qmax -максимальная поперечная сила у грани опоры;

       б) Q ≤ Оb1,        (93)

где Q - поперечная сила в конце наклонного сечения, начинающегося от опоры с длиной проекции с;

Qb1 - предельная поперечная сила, принимаемая равной Mb/с,
где Мb = φb4 (1 + φn) Rbt b h02 ,

но не менее        Qb,min= φb3 (1 + φn) Rbt b h0 ,        (94)

[при этом c = (φb4 / φb3) h0 ≈ 2,5 h0];

φb3, φb4 — см. табл. 29 п. 3.22;

φn — см. п. 3.22;

при этом, если в пределах длины с не образуются нормальные трещины [т.е. если М < Мcrc , где Мcrc определяется по формуле (164) п. 4.2 с заменой Rbt,ser на Rbt], Qb1 принимается не менее

       Qcrc = ,        (95)

где Sred - статический момент части приведенного сечения, расположенной по одну сторону от оси, проходящей через центр тяжести сечения, относительно этой оси;

τxy,crc - касательное напряжение на уровне центра тяжести приведенного сечения, соответствующее образованию наклонных трещин и определяемое из уравнения (183) п. 4.9 с заменой Rbt,ser на Rbt и Rb,ser на Rb; допускается значение τxy,crc = τ Rbt определять без учета напряжения σy с помощью графика на черт. 18.

График зависимости τ = f (σ)

-- для тяжелого бетона; ----- для мелкозернистого и легкого бетонов

При действии на элемент сосредоточенных или прерывистых нагрузок значения с при проверке условия (93) принимаются равными расстояниям от опоры до начала площадок опирания этих нагрузок (см. черт. 14).

При расчете элемента на действие равномерно распределенной нагрузки значение с принимается равным Мb1 /Qcrc (при этом Qb1 = Qcrc), а также равным длине приопорного участка l1, где не образуются нормальные трещины (при этом, если l1 > 2,5 h0, то Qb1 = Qb,min). В обоих случаях принимается Q = Qmax - q1 c (где q1 - см. п. 3.22).

РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ НА ДЕЙСТВИЕ
ИЗГИБАЮЩЕГО МОМЕНТА

3.31 (3.35). Расчет элементов на действие изгибающего момента для обеспечения прочности по наклонной трещине (черт. 19) должен производиться из условия

М ≤ (Rs Asp + Rs As) zs + Σ Rsw Asw zsw + Σ Rsw As,inc zs,inc ,        (96)

где М - момент от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения, относительно оси, перпендикулярной плоскости действия момента и проходящей через точку приложения равнодействующей усилий в сжатой зоне (черт. 20);

Σ Rsw Asw zsw, Σ Rsw As,inc zs,inc - суммы моментов относительной той же оси соответственно от усилий в хомутах и в отгибах, пересекающих растянутую зону наклонного сечения;

zs, zsw, zs,inc - расстояния от плоскостей расположения соответственно продольной арматуры, хомутов и отгибов до указанной выше оси.

Черт. 19. Схема усилий в наклонном сечении при расчете
по прочности на действие изгибающего момента

Черт. 20. Определение расчетного значения момента
при расчете наклонного сечения

а - для свободно опертой балки; б - для консоли

Высота сжатой зоны наклонного сечения, измеренная по нормали к продольной оси элемента, определяется из условия равновесия проекций усилий в бетоне сжатой зоны и в арматуре, пересекающей растянутую зону наклонного сечения, на продольную ось элемента согласно пп. 3.9 и 3.13. При этом принимается γs6 = 1,0, а в случае наличия в элементе отгибов в числителе выражения для х добавляется выражение ΣRsAs,inccosθ (где θ - угол наклона отгибов к продольной оси элемента).

Величину zs допускается принимать равной h0 — 0,5х, но не более h0-а′, если значение х вычислено с учетом сжатой арматуры.

Величина Σ Rsw Asw zsw при хомутах постоянной интенсивности определяется по формуле

       Σ Rsw Asw zsw = 0,5 qsw c2 ,        (97)

где qsw — см. п. 3.22;

с — длина проекции наклонного сечения на продольную ось элемента, измеренная между точками приложения равнодействующих усилий в растянутой арматуре и в сжатой зоне (см. п. 3.33).

Величина zs,inc для каждой плоскости отгибов определяется по формуле

       zs,inc = zs cos θ + (с - a) sin θ,        (98)

где а — расстояние от начала наклонного сечения до начала отгиба в растянутой зоне (см. черт. 19).

3.32. Расчет наклонных сечений на действие момента производится у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров, а также в местах обрыва или отгиба продольной арматуры в пролете.

Кроме того, расчет наклонных сечений на действие момента производится в местах резкого изменения конфигурации элементов (подрезки, узлы и т.п.).

Если наклонное сечение пересекает в растянутой зоне напрягаемую арматуру без анкеров на длине зоны передачи напряжений (см. п. 2.26) или ненапрягаемую арматуру без анкеров на длине зоны анкеровки (см. п. 5.32), значение расчетного сопротивления Rs соответствующей арматуры снижается путем умножения его на коэффициент условий работы γs3 , определяемый согласно поз. 3 табл. 23.

Расчет наклонных сечений на действие момента не производится, если выполняются условия п. 3.30.

3.33. Для свободно опертых балок невыгоднейшее наклонное сечение начинается от грани опоры и имеет длину проекции с при постоянной высоте сечения, равную:

               (99)

и принимаемую не более l1 — длины приопорного участка, на котором Q ≥ Q.crc (см. п. 3.30) или, если на нем образуются нормальные трещины, Q ≥ Qb1.

В формуле (99):

Q — поперечная сила в опорном сечении;

Fi, q — сосредоточенная и равномерно распределенная нагрузки в пределах наклонного сечения;

qsw — см. формулу (76) п. 3.22;

θ — угол наклона отгибов к продольной оси элемента.

Если значение с, определенное с учетом сосредоточенной силы Fi, оказывается меньше расстояния от грани опоры до этой силы Fi, а определенное без учета силы Fi — больше этого расстояния, то за значение с следует принимать расстояние до силы Fi.

Если в пределах длины с хомуты изменяют свою интенсивность с qsw1 у начала наклонного сечения на qsw2, то значение с определяется по формуле (99) при qsw = qsw2 и при уменьшении числителя на величину (qsw2 - qsw2)l1, где l1 - длина участка с интенсивностью хомутов qsw1.

Для балок, нагруженных равномерно распределенной нагрузкой q с постоянной интенсивностью хомутов без отгибов, условие (96) можно заменить условием

       ,        (100)

где М0 - момент в сечении по грани опоры;

Q - поперечная сила в опорном сечении.

Для консолей, нагруженных сосредоточенными силами, невыгоднейшее наклонное сечение начинается от мест приложения сосредоточенных сил вблизи свободного конца и имеет длину проекции с для консолей с постоянной высотой сечения, равную:

        ,        (101)

но не более расстояния от начала наклонного сечения до опоры. Здесь Q1 - поперечная сила в начале наклонного сечения.

Для консолей, нагруженных только равномерно распределенной нагрузкой q, невыгоднейшее наклонное сечение заканчивается в опорном сечении и имеет длину проекции с, равную:

        .        (102)

При этом, если с < l - lan или с < l - lp, то в формуле (102) принимается соответственно Rs As = 0 или Rs Asp = 0.

В формуле (102):

Аsp , А — площади сечения арматуры, доводимой до свободного конца;

lp , lan - длины зоны передачи напряжений и зоны анкеровки (см. пп. 2.26 и 5.32);

zs - определяется для опорного сечения.

Для элементов с высотой сечения, увеличивающейся с увеличением изгибающего момента, при определении длины проекции невыгоднейшего сечения по формуле (99) или (101) числители этих формул уменьшаются на величину (Rs Asp + Rs As)tgβ при наклонной сжатой грани и на величину (Rs Asp + Rs As)sinβ  при наклонной растянутой грани, где β - угол наклона грани к горизонтали.

3.34. Для обеспечения прочности наклонных сечений на действие изгибающего момента начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень полностью используется по моменту, не менее чем на h0/2, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб по расчету не требуется.

Примеры расчета

Пример 11. Дано: железобетонная плита перекрытия с размерами поперечного сечения по черт. 21; бетон тяжелый класса В25 (Rb = 13 МПа, Rbt = 0,95 МПа с учетом γb2 = 0,9, Еb = 27⋅103 МПа); ребро плиты армировано плоским каркасом с поперечными стержнями из арматуры класса Вр-I, диаметром 5 мм (Аsw = 19,6 мм2, Rsw = 260 МПа, Еs = 17⋅104 МПа), шагом s = 150 мм; усилие обжатия от растянутой продольной арматуры Р = 130 кН; временная эквивалентная нагрузка ν = 19 кН/м, нагрузка от собственного веса плиты и пола g = 4 кН/м; поперечная сила на опоре Qmax = 62 кН.

Черт. 21. К примеру расчета 11

Требуется проверить прочность по наклонной полосе ребра плиты между наклонными трещинами, а также прочность наклонных сечений по поперечной силе.

Р а с ч е т. h0 = 400 - 40 = 360 мм. Прочность бетона ребра плиты проверяем из условия (68).

Определим коэффициенты φw1 и φb1:

= 0,00154 ;

;

отсюда φw1 = 1 + 5αμw = 1 + 5⋅6,3⋅0,00154 = 1,0485 < 1,3;  φb1 = 1 - βRb = 1 - 0,01 ⋅ 13 = 0,87.

Тогда 0,3 φw1 φb1 Rb b h0 = 0,3 ⋅ 1,0485 ⋅ 0,87 ⋅ 13 ⋅ 85 ⋅ 360 = 108 700 H > Qmax = 62 кН, т.е. прочность бетона ребра плиты обеспечена.

Прочность наклонного сечения по поперечной силе проверяем из условия (71) п. 3.22.

Определим величины М и qsw:

φb1 = 2 (см. табл. 29) .

Так как b′f - b = 725 - 85 = 640 мм > 3h′f = 3 • 50 = 150 мм, принимаем b'f - b = 150 мм.

Тогда

.

Поскольку 1 + φf + φn = 1 + 0,184 + 0,447 > 1,5, принимаем 1 + φf + φn = 1,5 ;

Mb = φb2 (1 + φf + φn) Rbt b h02 = 2⋅1,5⋅0,95⋅85⋅3602 = 31,3 × 106 H⋅мм = 31,3 кН⋅м;

34 Н/мм.

Проверим условие (78):

Qb, min = φb3 (1 + φf + φn) Rbt b h0 = 0,6⋅1,5⋅0,95⋅85⋅360 = 26 163 H (где φb3 = 0,6, см. табл. 29);

       36,3 Н/мм > qsw = 34 Н/мм ,

т.е. условие (78) не выполняется;

следовательно, корректируем значение Мb:

Mb = 2h02 qsw φb2 / φb3 = 2 ⋅ 3602 ⋅ 34= 29,38 ⋅ 106 H⋅мм = 29,4 кН⋅м и принимаем с0 = 2h0 = 2 ⋅ 360 = 720 мм.

Определим длину проекции невыгоднейшего наклонного сечения с:

q1 = g + ν/2 = 4 + 19/2 = 13,5 кН/м (Н/мм).

Так как 0,56 qsw = 0,56 ⋅ 34 = 19 Н/мм > q1 = 13,5 Н/мм, значение с равно:

= 1,475 м.

Поскольку = 1,2 м < с= 1,475 м, принимаем с = 1,2 м и Qb = Qb,min = 26,16 кН.

Проверяем условие (71), принимая Q в конце наклонного сечения, т.е. Q = Qmax - q1c = 62 - 13,3 • 1,2 = 45,8 кН;

Qb + qsw c0 = 26,46 + 34 • 0,72 = 50,6 кН > Q = 45,8 кН,

т.е. прочность наклонного сечения обеспечена.

При этом s = 150 мм <

       = 366 мм

и, кроме того, s < h/2 = 400/2 = 200 мм, т.е. требования пп. 3.21 и 5.42 выполнены.

Пример 12. Дано: свободно опертый железобетонный ригель перекрытия пролетом l = 8,3 м нагружен равномерно распределенной нагрузкой: временной эквивалентной ν = 114 кН/м и постоянной g = 46 кН/м; размеры поперечного сечения: b = 300 мм, h = 800 мм, h0 = 700 мм; бетон тяжелый класса В30 (Rb = 15,5 МПа, Rbt = 1,1 МПа с учетом γb2 = 0,9); хомуты сварные из арматуры класса А-III (Rsw = 290 МПа); усилие предварительного обжатия Р = 1600 кН.

Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии от опоры и как может быть увеличен их шаг.

Р а с ч е т. Наибольшая поперечная сила в опорном сечении равна:

= 664 кН ,

где q = ν + g = 114 + 46 = 160 кН/м.

Определим требуемую интенсивность хомутов приопорного участка согласно п. 3.23б.

Поскольку φn = 0,1 = 0,693 > 0,5,

то принимаем „ = 0,5.

Из формулы (73) при φf = 0 и φb2 = 2 (см. табл. 29) получаем:

Mb = φb2 (1 + φn) Rbt b h02 = 2⋅1,5⋅1,1⋅300⋅700 = 485•10 H⋅мм = 485 кН⋅м;

q1 = g + ν/2 = 46 + 114 / 2 = 103 кН/м (Н/мм);

Qb1 = 2 = 447 кН.

Так как = 745 кН > Qmax = 664 кН,

интенсивность хомутов определяется по формуле

= 124,3 Н/мм.

При этом = 155 > qsw = 124,3 Н/мм,

следовательно, принимаем qsw = 155 Н/мм.

Согласно п. 5.42, шаг у опоры должен быть не более 1/3h = 800/3 = 267 мм и не более 500 мм, а в пролете - не более 3/4h = 600 мм и не более 500 мм. Максимально допустимый шаг у опоры, согласно формуле (67), равен:

= 548 мм.

Принимаем шаг хомутов у опоры s1 = 250 мм, а в пролете - 2s1 = 500мм.

Отсюда Аsw = qsw s / Rsw = 155 • 250/290 = 134 мм2.

Принимаем в поперечном сечении два хомута диаметром 10 мм (Asw = 157 мм2).

Тогда = 182 Н/мм ;

       qsw2 = 0,5qsw1 = 91 Н/мм.

Длину участка с наибольшей интенсивностью хомутов qsw1 определяем согласно п. 3.24.

Так как qsw1 - qsw2 = 182 - 91 = 91 Н/мм < q1 = 103 Н/мм, значение с равно:

6,36 м > = 2,33 м.

Принимаем с = 2,33 м.

По формуле (77) при qsw = qsw1 = 182 Н/м вычисляем c01:

= 1,632 м.

Тогда         =

1,45 м < = 2,08 м.

Принимаем длину участка с шагом хомутов s = 250 мм не менее 2,08 м.

Пример 13. Дано: железобетонная балка покрытия, нагруженная сосредоточенными силами, как показано на черт. 22, а; размеры поперечного сечения — по черт. 22, б; бетон тяжелый класса В50 (Rbt = 1,4 МПа при γb2 = 0,9); хомуты из арматуры класса A-III (Rsw = 285 МПа); усилие предварительного обжатия Р = 640 кН.

Черт. 22. К примеру расчета 13

Требуется определить диаметр и шаг хомутов, а также выяснить, на каком расстоянии и как может быть увеличен их шаг.

Р а с ч е т. Сначала определим, согласно п. 3.22, величину Мb:

φb2 = 2 (см. табл. 29); h'f = 150 + 100/2 = 200 мм (см. черт. 22,б);

b'f - b = 280 - 80 = 200 мм < 3h′f; h0 = 890 - 90 = 800 мм;

0,469 < 0,5 ;

= 0,714 > 0,5 .

Принимаем φn = 0,5.

Поскольку 1 + φf + φn > 1,5, принимаем 1 + φf + φn = 1,5, Mb = φb2 (1 + φf + φn) Rbt b h02 = 2 ⋅ 1,5 ⋅ 1,4 ⋅ 80 ⋅ 8002 = 215 ⋅ 106 Н⋅мм = 215 кН⋅м.

Определим требуемую интенсивность хомутов согласно п. 3.23а, принимая длину проекции наклонного сечения с равной расстоянию от опоры до первого груза - с1 = 1,3 м.

Поперечная сила на расстоянии c1 от опоры равна Q1 = 288,6 кН (см. черт. 22, a).

Из формулы (72) имеем

164,5 кН > Qb,min = φb3 (1 + φf + φn) Rbt b h0 =
= 0,6 ⋅ 1,5 ⋅ 1,4 ⋅ 80 ⋅ 800 = 80,64 кН.

Тогда        x1 = = 0,75.

Поскольку c1 = 1,3 м < 2h0 = 2 ⋅ 0,8 = 1,6 м, принимаем c0 = c1 = 1,3 м;

x01 = = 0,396 .

Так как x01 = 0,396 < x1 = 0,75 < = 1, значения qsw(1) определяем по формуле (80):

qsw(1) = = 94,8 кН/м.

Определим qsw(2) при значении с, равном расстоянию от опоры до второго груза, с2 = 2,8 м:

= 76,8 кН < Qb,min = 80,64 кН.

Принимаем Qb2 = 80,64 кН.

Соответствующая поперечная сила равна Q2 = 205,2 кН.

Поскольку c2 = 2,8 м > 2h0 = 1,6 м, принимаем c0 = 2h0 = 1,6 м;

1;

= 1,75.

Следовательно, значение qsw(2) определяем по формуле (80):

77,85 кН/м.

Принимаем максимальное значение qsw = qsw(1) = 94,8 кН•м.

Согласно п. 5.42, шаг s1 у опоры должен быть не более 1/3h = 890/3 = 297 мм и не более 500 мм, а в пролете — не более 3/4h = 3/4 • 890 = 667 мм и не более 500 мм. Максимально допустимый шаг у опоры, согласно формуле (67), равен:

smах = φb4 (1+φn) Rbtbh02 / Qmax = 1,5⋅1,5⋅1,4⋅80⋅8002/294,6⋅103 = 547 мм.

Принимаем шаг хомутов у опоры s1 = 150 мм, а в пролете — s2 = 2s1 = 300 мм.

Отсюда         = 50 мм2 .

Принимаем одноветвевые хомуты диаметром 8 мм (Аsw = 50,3 мм2).

Длину участка с шагом s1 определяем из условия обеспечения прочности согласно п. 3.24.

При этом = 95,6 Н/мм; qsw2 = 0,5 qsw1 = 47,8 Н/мм; qsw1 - qsw2 = qsw2 = 47,8 Н/мм.

Зададим длину участка с шагом хомутов s1 = 150 мм равной расстоянию от опоры до второго груза l1 = 2,8 м и проверим условие (71) при значении с, равном расстоянию от опоры до третьего груза: с = 4,3 м >l1.

Значение c01 определим по формуле (77) при qsw = qsw1 = 95,6 кН/м:

= 1,5 м < 2h0 = 1,6 м .

Так как с01 = 1,5 м = с - l1 = 4,3 - 2,8 = 1,5 м, выражение qswc0 заменим выражением qsw2 (c - l1) = 47,6 ⋅ 1,5 = 71,4 кН.

Qb = Мb/с = = 50 кН < Qb,min = 80,64 кН.

Принимаем Qb = Qb,min = 80,64 кН.

Соответствующая поперечная сила равна Q3 = 121,8 кН (см. черт. 22, a).

Qb + qswc0 = 80,64 + 71,4 = 152,04 кН > Q3 = 121,8 кН,

т. е. прочность наклонного сечения обеспечена.

Таким образом, длину участка с шагом хомутов s1 = 150 мм принимаем равной l1 = 2,8 м.

Пример 14. Дано: плита перекрытия с растянутой гранью, наклонной к горизонтали, с размерами по черт. 23; бетон тяжелый класса В40 (Rbt = 1,25 МПа с учетом γb2 = 0,9); хомуты вертикальные класса А-III, диаметром 8 мм (Rsw = 285 МПа, Asw = 50,3 мм2) и шагом s = 100 мм; усилие предварительного обжатия Р = 980 кН; временная эквивалентная нагрузка ν = 24,2 кН/м; постоянная нагрузка g = 7,8 кН/м; поперечная сила на опоре 186 кН.

Требуется проверить прочность наклонного сечения по поперечной силе.

Черт. 23. К примеру расчета 14

Р а с ч е т    ведем согласно п. 3.27.

Из черт. 23 имеем h03 = 300 — 75 = 225 мм. Размер b принимаем на уровне середины высоты опорного сечения:

= 233 мм.

Определим для опорного сечения величины φfs, φns и Mbs по формулам (74), (75), (73):

b'f - b = 3h′f = 3 • 60 = 180 мм;

= 0,154 ;

= 1,495 > 0,5 .

Принимаем 1 + φfs + φns = 1,5 ; φb2 = 2 (см. табл. 29);

Mbs = φb2 (1 + φfs + φns) Rbt b h02 = 2 ⋅ 1,5 ⋅ 1,25 ⋅ 233 ⋅ 2252 = 44,2 • 106 H⋅мм.

Определим величины qsw и qinc, принимая tgβ = tgβ1 = 0,0815:

= 143,3 Н/мм ;

qinc = φb2 (1 + φfs + φns) Rbt b tg2β = 2⋅ 1,5 ⋅ 1,25 ⋅ 233 ⋅ 0,08152 = 5,8 Н/мм;

q1 = g + ν/2 = 7,8 + 24,2/2 = 19,9 кН/м (Н/мм).

Проверим условие (87):

0,56 qsw - 2,5 = 0,56 ⋅ 143,3 - 2,5 =
= 21,1 Н/мм > q1 = 19,9 Н/мм.

Условие (87) выполняется, и, следовательно, невыгоднейшее значение с определяем по формуле (88) :

= 901 мм.

Рабочая высота поперечного сечения на расстоянии с = 901 мм от опоры равна:

h0 = h0s + ctgβ = 225 + 901 ⋅ 0,0815 = 298мм,

а ширина ребра на уровне середины высоты h = 298+75 = 373 мм равна

= 226 мм.

Поскольку = 993 мм > с = 901 мм, оставляем с = 901 мм.

Определим соответствующее значение Мb, принимая 1+φfs+φns = 1,5:

Мb = 2 ⋅ 1,5 ⋅ 1,25 ⋅ 226 ⋅ 2982 = 75,2 ⋅ 106 H ⋅ мм.

Значение c0 равно:

= 725 мм > 2h0 = 2 ⋅ 298 = 596 мм.

Принимаем с0 = 596 мм.

Проверяем условие (71), принимая поперечную силу в конце наклонного сечения равной Q = Qmax - q1c = 186 — 19,9 ⋅ 0,901 = 168,1 кН:

= 83,5 ⋅ 103 Н ;

Qb + qswc0 = 83,5 + 143,3 ⋅ 0,596 = 168,9 кН > Q = 168,1 кН,

т. е. прочность наклонного сечения обеспечена.

Пример 15. Дано: железобетонная двускатная балка покрытия с размерами по черт. 24 загружена сосредоточенными силами от плит покрытия и подвесных кранов, как показано на черт. 24,б; бетон тяжелый класса В40 (Rbt = 1,55 МПа при γb2 = 1,1); хомуты двухветвевые из арматуры класса А-III, диаметром 10 мм (Rsw = 290 МПа, Аsw = 101 мм2) и шагом s = 150 мм; усилие предварительного натяжения Р = 1220 кН.

Требуется проверить прочность наклонных сечений по поперечной силе.

Черт. 24. К примеру расчета 15

Р а с ч е т    ведем согласно п. 3.26. Проверим прочность наклонного сечения с длиной проекции, равной расстоянию от опоры до первого груза — с1 = 1,35 м.

Рабочая высота поперечного сечения в конце наклонного сечения равна:

h0 = 800 - 80 + 1350/12 = 832 мм.

Определим значение Мb согласно п. 3.22:

φb2 = 2 (см. табл. 29); h′f = 160 + 50/2 = 185 мм;

b′f - b = 400 - 80 = 320 мм < 3h′f = 3 • 185 = 555 мм;

= 0,667 > 0,5 .

Принимаем φf = 0,5;

= 1,18 > 0,5 .

Принимаем φn = 0,5.

Поскольку 1 + φf + φn > 1,5, принимаем 1 + φf + φn = 1,5;

Mb = φb2 (1 + φf + φn) Rbt b h02 = 2 ⋅ 1,5 ⋅ 1,55 ⋅ 80 ⋅ 8322 = 257⋅106 H⋅мм = = 257 кН⋅м.

Значение qsw равно:

= 303 Н/мм.

По формуле (77) определим длину проекции наклонной трещины:

= 921 мм = 0,921 м.

Так как с01 = 0,921 м < с1 = 1,35 м и с01 < 2h0 = 2 ⋅ 0,832 = 1,664 м, оставляем c01 = 0,921 м.

Проверим условие (72), приняв Q в месте первого груза - Q1 = 445 кН:

180,4 кН ;

Qb + qswc01 = 190,4 + 303 ⋅ 0,91 = 470 кН > Q1 = 445 кН,

т.е. прочность этого наклонного сечения обеспечена.

Аналогично проверим прочность наклонного сечения с длиной проекции, равной расстоянию от опоры до второго груза — с2 = 2,85м:

h0 = 720 + 2850 / 12 = 957 мм.

Поскольку = 3,19 м > c2 = 2,85 м, оставляем c2 = 2,85 м.

1 + φfs + φns = 1,5 ;

Мb = 2 ⋅ 1,5 ⋅ 1,55 ⋅ 80 ⋅ 9572 = 341 ⋅ 106 Н ⋅ мм;

= 1060 мм < с2 = 2,85 м ;

с02 < 2h0 = 2 ⋅ 0,957 = 1,914 м.

Оставляем c02 = 1060 мм;

H > Q2 = 400 кН ,

т.е. прочность этого наклонного сечения также обеспечена.

Пример 16. Дано: многопустотная плита перекрытия пролетом l = 5,85 м с поперечным сечением по черт. 25; бетон тяжелый класса В25 (Rbt = 0,95 МПа с учетом γb2 = 0,9 , Eb = 27 ⋅ 103 МПа); усилие обжатия от каждого растянутого стержня Р = 69,2 кН; характеристики приведенного сечения шириной 0,2 м: площадь Аred = 24,7 ⋅ 103 мм2; момент инерции Ired = 183,3 ⋅ 106 мм4; расстояние от центра тяжести до растянутой грани у0 = 107 мм; временная эквивалентная нагрузка y = 12 кН/м2; нагрузка от собственного веса плиты и пола g = 6 кН/м2.

Требуется выяснить, необходима ли в плите поперечная арматура.

Черт. 25. К примеру расчета 16

Р а с ч е т. Проверим условия прочности согласно п. 3.30:

h0 = 220 - 20 = 200 мм.

Расчет ведем для ширины плиты, равной расстоянию между центрами круглых отверстий, т.е. b′f = 200 мм, b = 40 мм.

Тогда        q = (6 + 12)0,2 = 3,6 кН/м = 3,6 Н/мм;

       q1 = (6 + 12/2)0,2 = 2,4 кН/м = 2,4 Н/мм.

Поперечная сила в опорном сечении = 10,52 кН.

Проверим условие (92):

2,5Rbt b h0 = 2,5 • 0,95 • 40 • 200 = 19 000 H > Qmax = 10,52 кН,

т. е. условие (92) выполняется.

Проверим условие (93), принимая значение с равным Мb1 / Qcrc и длине участка l1 без нормальных трещин. Для этого определим значение Mb1 и Qcrc, принимая

= 0,63 > 0,5 ,

т.е. φn = 0,5 и φb4 = 1,5 (см. табл. 29).

Mb1 = φb4 (1 + φn) Rbt b h02 = 1,5(1 + 0,5)0,95 ⋅ 40 ⋅ 2002 = 3,42 ⋅ 106 H⋅мм.

Статический момент части сечения, расположенной выше оси, проходящей через центр тяжести, Sred равен:

936 ⋅ 103 мм3 ,

где D = 160 мм (см. черт. 25).

Из графика на черт. 18

при         = 2,95

находим τ = 1,99, т.е. τxy,crc = τ Rbt = 1,99 ⋅ 0,95 = 1,89 МПа .

Тогда = 14,8 ⋅ 103 Н.

Поскольку Qmax = 10,52 кН < Qcrc = 14,8 кН, прочность наклонного сечения с длиной проекции с = Mb1 / Qcrc заведомо обеспечена.

Определим длину участка l1 без нормальных трещин, т.е. расстояние от опоры до нормального сечения, в котором

Определим момент Mcrc согласно п. 4.2, принимая в целях упрощения расчета Wpl = 1,5 Wred и φ = 0,8:

1,72 ⋅ 106 мм3 ;

Wpl = 1,5 ⋅ 1,72 ⋅ 106 = 2,58 ⋅ 106 мм3 ;

= 55,7 мм ;

е0 = y0 - a = 107 - 20 = 87 мм ;

Mcrc = P(e0 + r) + Rbt Wpl = 69,2 • 103 (87 + 55,7) + 0,95 ⋅ 2580 ⋅ 103 =
= 12,33 ⋅ 103 H ⋅ мм.

Из вышеприведенного квадратного уравнения находим с = l1 :

= 1,622 м > 2,5 h0 = 2,5 ⋅ 0,2 = 0,5м.

Следовательно,

Qb1 = Qb,min = φb3 (1 + φn) Rbt b h0 = 0,6 ⋅ 1,5 ⋅ 0,95 ⋅ 40 ⋅ 200 = 6840 H.

Поперечная сила в конце наклонного сечения равна:

Q = Qmax - q1c = 20,32 - 2,4 ⋅ 1,622 = 6,41 кН < Qb1 = 6,84 кН,

т.е. условие (93) выполнено. Следовательно, поперечную арматуру в плите можно не устанавливать.

Пример 17. Требуется по данным примера 11 проверить прочность наклонных сечений на действие изгибающего момента, принимая растянутую продольную арматуру ребра плиты в виде одного напрягаемого стержня класса A-V, диаметром 22 мм (Rs = 680 МПа, Аsp = 380 мм2) и одного ненапрягаемого стержня класса Вр-I, диаметром 5 мм (Rs = 360 МПа, Аs = 19,6 мм2); оба стержня постоянных анкеров не имеют; передаточная прочность бетона Rbp = 15 МПа; предварительное напряжение стержня с учетом потерь от релаксации и от технологических анкеров σsp1 = 660 МПа (потери от температурного перепада, трения и деформации форм равны нулю); длина площадки опирания lsup = 150 мм; характеристики приведенного сечения: площадь Аred = 68 800 мм2, момент инерции Ired = 1125 ⋅ 106 мм4, расстояние от центра тяжести до растянутой грани у0 = 275 мм.

Р а с ч е т    производим согласно пп. 3-31-3.33. Поскольку продольная арматура не имеет анкеров, расчетное сопротивление арматуры Rs определяем с учетом коэффициента условий работы γb5 согласно поз. 3 табл. 23. Начало наклонного сечения принимаем у грани опоры. Следовательно, lx = lsup = 150 мм. Для напрягаемого стержня длину передачи напряжений lр определяем по формуле (19). Из табл. 24 имеем ωp = 0,25, λp = 10. Поскольку Rs = 680 МПа > σsp1 = 660 МПа, принимаем σtp = Rs = 680 МПа.

= 469 мм > 15d =
= 15⋅22 = 330 мм.

Оставляем lp = 469 мм.

Отсюда для напрягаемого стержня = 0,32 и Rs = 680γs5 = 680 ⋅ 0,32 = 218 МПа.

Для ненапрягаемого стержня длину анкеровки определяем по формуле (301) п. 5.32. Поскольку стержень располагается в сжатом от действия опорной реакции бетоне, принимаем ωan = 0,5; Δλan = 8;

102 мм < 200 мм.

Принимаем lan = 200 мм. Тогда:

= 0,7 ;

Rs = 360 γs5 = 360 ⋅ 0,7 = 252 МПа .

Высоту сжатой зоны х определяем как для прямоугольного сечения по формуле (26), принимая γs6 = 1, b = b'f = 725 мм, A'sp = 0 и A′s = 0:

= 9,3 мм < h′f = 50 мм.

Тогда z = h0 - 0,5x = 360 - 0,5 ⋅ 9,3 = 355,2 мм. Из примера 11 имеем qsw = 34 Н/мм.

Определим длину проекции невыгоднейшего наклонного сечения по формуле (99), принимая Fi = 0, As,inc = 0, q = ν + g == 19 + 4 = 23 Н/мм = 23 кН/м:

= 1088 мм.

Определим длину приопорного участка l1, на котором Q ≥ Qcrc, т.е. из уравнения Q = Qmax - q1l1 = Qcrc.

Вычисляем значение Qcrc согласно п. 3.30. Из графика на черт. 18 при

= 1,99

находим τ = 1,73, т.e. τxy,crc = Rbt τ = 0,95 ⋅ 1,73 = 1,64 МПа. Статический момент Sred равен:

Sred = b (h - y0)2 / 2 + (b'f - b)h'f(h - y0 -h'f/2) = 85(400 - 275)2/2 +

+ (725 - 85)50(400 - 275 - 50/2) = 38 640 ⋅ 103 мм3.

Тогда = 40,7 ⋅ 103 H ;

= 1,58 мм.

Поскольку с = 1,088 м < l1 = 1,58 м, значение с не корректируем.

Момент внешних сил относительно оси, проходящей через точку приложения равнодействующей усилий в сжатой зоне, в данном случае равен изгибающему моменту в нормальном сечении, проходящем через указанную ось, т.e. на расстоянии (lу + с) от точки приложения опорной реакции, где lу = lsup / 3 = 50 мм — расстояние от этой точки до конца закладной детали (черт. 26):

Черт. 26. К примеру расчета 17

=
= 55,6 кН ⋅ м.

Проверяем прочность из условия (96), с учетом формулы (97):

(Rs Asp + Rs As)zs + 0,5 qsw c2 = (218⋅380 + 252⋅19,6) 355,2 + 0,5⋅34⋅10882 = 31,2 ⋅ 106 +20,1 ⋅ 106 = 51,3 ⋅ 106 H⋅мм = 51,3 кН⋅м < М = 55,6 кН⋅м,

т.е. прочность наклонных сечений на действие изгибающего момента не обеспечена.

Добавляем на приопорном участке дополнительную сетку длиной l1 = 300 мм с поперечными стержнями того же диаметра и шага, что и в основном плоском каркасе, и снова проверяем прочность сечения. Тогда, согласно п. 3.33, имеем:

qsw2 = qsw = 34 Н/мм; qsw1 - qsw2 = qsw = 34 Н/мм ;

= 909 мм ;

ly + с = 50 + 909 = 959 мм;

M = 62 ⋅ 0,959 = 48,9 кН⋅м .

Проверяем условие (96), принимая

Σ Rsw Asw zsw = 0,5 qsw2 c2 + (qsw2 - qsw1)l1(c - l1/2) = 0,5 ⋅ 34 ⋅ 9092 +
+ 34 ⋅ 300 (909 - 150) = 21,8 ⋅ 106 H⋅мм = 21,8 кН⋅м;

(Rs Asp + Rs As) zs + Σ Rsw Asw zsw = 31,2+21,8 = 53 кН⋅м > М = 48,9 кН⋅м,

т.е. прочность наклонного сечения обеспечена.

Внецентренно сжатые элементы

ОБЩИЕ ПОЛОЖЕНИЯ

3.35 (1.21). При расчете по прочности внецентренно сжатых железобетонных элементов должен приниматься во внимание случайный эксцентриситет еа, обусловленный не учтенными в расчете факторами. Эксцентриситет еа в любом случае принимается не менее:

1/600 всей длины элемента или расстояния между его сечениями, закрепленными от смещения;

1/30 высоты сечения элемента;

10 мм (для конструкций, образуемых из сборных элементов, при отсутствии других экспериментально обоснованных значений еа).

Для элементов статически неопределимых конструкций (в том числе для колонн каркасных зданий) значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения е0 принимается равным эксцентриситету, полученному из статического расчета конструкций, но не менее еа.

В элементах статически определимых конструкций (например, фахверковые стойки, стойки ЛЭП) эксцентриситет е0 находится как сумма эксцентриситетов — определяемого из статического расчета конструкции и случайного.

3.36 (3.19, 3.3). При расчете внецентренно сжатых элементов необходимо учитывать влияние на их несущую способность прогибов в плоскости эксцентриситета продольного усилия (плоскости изгиба) и в нормальной к ней плоскости согласно указаниям п. 3.39. В случае расчета из плоскости изгиба значение е0 принимается равным значению случайного эксцентриситета.

Расчет из плоскости изгиба можно не производить, если гибкость элемента l0/i (для прямоугольных сечений - l0/h) в плоскости изгиба превышает гибкость в плоскости, нормальной к плоскости изгиба.

При наличии расчетных эксцентриситетов в двух направлениях, превышающих случайные эксцентриситеты еа, производится расчет на косое внецентренное сжатие.

3.37. Для наиболее часто встречающихся видов сжатых элементов (прямоугольного и двутаврового сечений с симметричной арматурой, сосредоточенной у наиболее сжатой и у растянутой граней, кольцевого сечения с арматурой, равномерно распределенной по окружности) расчет по прочности нормальных сечений при расположении продольной силы в плоскости симметрии производится согласно пп. 3.41—3.43. При этом граничное значение относительной высоты сжатой зоны ξR, коэффициент условий работы арматуры γs6 и напряжение σsc в напрягаемой арматуре, расположенной в сжатой зоне, определяются как для изгибаемых элементов согласно пп. 3.6-3.8.

Для других видов сечений, а также при косом внецентренном сжатии расчет нормальных сечений производится по формулам общего случая расчета нормальных сечений изгибаемых элементов согласно п. 3.18; при этом в правую часть уравнения (61) добавляется значение N, а за М в условии (60) принимается момент продольной силы N относительно оси, параллельной прямой, ограничивающей сжатую зону и проходящей через центр тяжести сечения растянутого стержня, наиболее удаленного от указанной прямой.

3.38. Расчет по прочности наклонных сечений внецентренно сжатых элементов производится аналогично расчету изгибаемых элементов в соответствии с указаниями пп. 3.19-3.34, учитывая влияние продольной силы N путем добавления ее к значению Р в формуле (75). При этом влияние продольных сил не учитывается, если они создают изгибающие моменты, одинаковые по знаку с моментами от действия поперечной нагрузки. Для внецентренно сжатых элементов статически неопределимых конструкций, при статическом расчете которых принимается, что продольная сила располагается в центре тяжести сечения, допускается всегда учитывать влияние продольных сил.

УЧЕТ ВЛИЯНИЯ ПРОГИБА ЭЛЕМЕНТА

3.39 (3.24, 3.6). При расчете внецентренно сжатых элементов следует учитывать влияние прогиба на их несущую способность, как правило, путем расчета конструкций по деформированной схеме, принимая во внимание неупругие деформации материалов и наличие трещин.

Допускается производить расчет конструкций по недеформированной схеме, учитывая при гибкости l0/i > 14 влияние прогиба элемента путем умножения эксцентриситета е0 на коэффициент η, определяемый по формуле

                ,        (103)

где Nсr — условная критическая сила, принимаемая равной :

,        (104)

где I, Is — моменты инерции соответственно бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения;

φl — коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии, равный:

                ,        (105)

но не более 1 + β,

здесь β — коэффициент, принимаемый в зависимости от вида бетона по табл. 30;

M1,  M1 l — моменты внешних сил относительно оси, проходящей через центр тяжести крайнего ряда арматуры, расположенного у растянутой (менее сжатой) грани, параллельной этой грани, соответственно от действия полной нагрузки и от действия постоянной и длительной нагрузок;

δe — коэффициент, принимаемый равным e0/h, но не менее

       δe,min = 0,5 - 0,01 - 0,01 Rb ,        (106)

здесь Rb — в МПа, допускается принимать при γb2 = 1,0;

l0 — принимается по указаниям п. 3.40,

φp — коэффициент, учитывающий влияние предварительного напряжения арматуры на жесткость элемента; при равномерном обжатии сечения напрягаемой арматурой φp определяется по формуле

               ,        (107)

здесь σbp — определяется с учетом всех потерь при коэффициенте γsp<1,0;

— принимается не более 1,5;

Rb — принимается без учета коэффициентов условий работы.

Для круглых и кольцевых сечений за величину h в формулах (106) и (107) принимается диаметр сечения D.

При гибкости l0/i ≤ 35 (для прямоугольных сечений - при l0/h ≤ 10) и при μ < 0,015 допускается принимать

               .

Таблица 30 (30)

П р и м е ч а н и е. Группы мелкозернистого бетона приведены в п. 2.1.

Для элементов из мелкозернистого бетона группы Б в формулу (104) вместо значения 6,4 подставляется 5,6.

При N ≥ Ncr следует увеличивать размеры сечения.

При расчетных эксцентриситетах в двух направлениях коэффициент η определяется отдельно для каждого направления и умножается на соответствующий эксцентриситет.

3.40. Для внецентренно сжатых элементов, имеющих несмещаемые опоры (например, фахверковые стойки), а также для элементов, не связанных с другими конструкциями (например, стойки ЛЭП), расчетные длины l0 определяются из расчета на устойчивость.

Расчетные длины колонн одноэтажных и многоэтажных зданий принимаются согласно указаниям «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры».

РАСЧЕТ ЭЛЕМЕНТОВ СИММЕТРИЧНОГО СЕЧЕНИЯ
ПРИ РАСПОЛОЖЕНИИ ПРОДОЛЬНОЙ СИЛЫ
В ПЛОСКОСТИ СИММЕТРИИ

ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ
С СИММЕТРИЧНОЙ АРМАТУРОЙ

3.41. Расчет прямоугольных течений с симметричной арматурой (черт. 27), сосредоточенной у наиболее сжатой и у растянутой (менее сжатой) граней элемента, производится в зависимости от относительной высоты сжатой зоны следующим образом:

        :        (108)

Черт. 27. Схема усилий в прямоугольном сечении внецентренно сжатого железобетонного элемента

а) при ξ1 ≤ ξR (см. табл. 26 и 27 - из условия

Ne ≤ Rb bx (h0 - 0,5 х) + σsc A′sp (h0 - a′p) + RscA′s(h0 - a′s) ,        (109)

где         .        (110)

Коэффициент γs6 определяется no формуле (27), принимая ξ1 по формуле (108) и ; допускается коэффициент γs6 определять по формуле (23) п. 3.7, принимая ξ = ξ1 ;

б) при ξ1 > ξR — также из условия (109); при этом, если применяется арматура с условным пределом текучести (см. п. 2.16), высота сжатой зоны х определяется по формуле

        ,        (111)

где ξel — определяется по формуле

        ,

здесь ω, σsc,u и σsp — см. п. 3.6;

β — см. п. 3.18; при β = 0,8, т.е. при электротермическом и электротермомеханическом неавтоматизированных способах натяжения арматуры классов A-IV, A-V и A-VI, а также для прочих классов арматуры при любом способе натяжения значение можно определить по табл. 31 (для элементов из тяжелого бетона) или по табл. 32 (для элементов из легкого бетона или мелкозернистого бетона группы А).

Таблица 31

Окончание табл. 31

σsp - предварительное напряжение при коэффициенте γsp < 1,0 (см. п. 1.18);

ω = 0,85 - 0,008 Rb ; ; .

Таблица 32

ω = 0,8 - 0,008 Rb ; ; .

Если значение х, определенное по формуле (111), оказывается больше ξelh0, то в условие (109) подставляется значение х, равное:

        ,        (112)

где        ;

                       .

Значения ω и можно определял, по табл. 31 или 32.

При наличии ненапрягаемой арматуры S и S' с условным пределом текучести следует учитывать примечание к п. 3.3, распространяя его и на арматуру S'.

Если используется напрягаемая арматура с физическим пределом текучести, высота сжатой зоны х при ξ > ξR всегда определяется по формуле (112).

Значение е вычисляется по формуле

               е = e0 + .        (113)

При этом эксцентриситет e0 определяется с учетом прогиба элемента согласно пп. 3.39 и 3.40.

П р и м е ч а н и е. При большом количестве ненапрягаемой арматуры с физическим пределом текучести (при RsAs > 0,2 RsAsp) не следует пользоваться формулами (111) и (112). В этом случае высота сжатой зоны х определяется по формулам общего случая согласно п. 3.18 с учетом п. 3.37.

ДВУТАВРОВЫЕ СЕЧЕНИЯ С СИММЕТРИЧНОЙ АРМАТУРОЙ

3.42. Расчет двутавровых сечений с симметричной арматурой, сосредоточенной в полках, производится следующим образом.

Если граница сжатой зоны проходит в полке, т.е. соблюдается условие

       N ≤ Rb b'f h'f - Аsр (γs6Rs - σsc)        (114)

(где γs6 определяется по формуле (23) при ξ = h′f / h0), то расчет производится как для прямоугольного сечения шириной b'f в соответствии с указаниями п. 3.41.

Если граница сжатой зоны проходит в стенке, т.е. условие (114) не соблюдается, то расчет производится в зависимости от относительной высоты сжатой зоны следующим образом:

       ;        (115)

а) при ξ1 ≤ ξR (см. табл. 26 или 27) прочность сечения проверяется из условия

Ne ≤ Rb bx (h0 - 0,5x) + RbAoν(h0 - 0,5h′f) + σscA′sp(h0 - a′p) +

               + RscA′s (h0 - a′s),        (116)

где         .        (117)

Здесь γs6 определяется по формуле

       ,        (118)

где η - см. п. 3.7;

        ;        (119)

при N > Rb Aoν допускается γs6 вычислять по формуле (23) п. 3.7, принимая ξ = ξ1 ;

б) при ξ1 > ξR прочность сечения проверяется также из условия (116), при этом высота сжатой зоны х при арматуре с условным пределом текучести (см. п. 2.16) определяется по формуле

.        (120)

В формулах (115) - (120):

Аoν — площадь сечения сжатых свесов полки, равная:

       Аoν  = (b'f - b) h'f ;

ξel  — см. п. 3.41;

β — см. п. 3.18.

Если значение х, определенное по формуле (120), оказывается больше ξelh0, то в условие (116) подставляется значение х, равное:

       ,        (121)

где        t = ,

Rs, ω - см. табл. 31 или 32.

При напрягаемой арматуре с физическим пределом текучести высота сжатой зоны х при ξ1 > ξR всегда определяется по формуле (121).

При наличии ненапрягаемой арматуры S и S′ с условным пределом текучести следует учитывать примечание к п. 33, распространяя его и на арматуру S'.

П р и м е ч а н и я:  1. При переменной высоте свесов полки значение h′f принимается равным средней высоте свесов.

2. При большом количестве ненапрягаемой арматуры е физическим пределом текучести (при RsAs > 0,2 RsAsp) не следует пользоваться формулами (120) и (121). В этом случае высота сжатой зоны определяется по формулам общего случая, согласно п. 3.18, с учетом п. 3.37.

КОЛЬЦЕВЫЕ СЕЧЕНИЯ

3.43 (3.21). Расчет элементов кольцевого сечения (черт. 28) при соотношении внутреннего и наружного радиусов r1/r2 ≥ 0,5 с арматурой, равномерно распределенной по окружности (при числе продольных стержней не менее шести), должен производиться из условия

Черт. 28. Схема, принимаемая при расчете кольцевого сечения

Ne0 ≤ (Rb Arm + Rsc Asp,tot rsp + Rsc As,tot rs) +

       + Rs Asp,tot φsp zsp + Rs As,tot φs zs ,        (122)

где rm = 0,5 (r1 + r2) ;

Asp,tot — площадь сечения всей напрягаемой продольной арматуры;

As,tot — то же, ненапрягаемой арматуры;

rsp, rs — радиусы окружностей, проходящих через центры тяжести стержней, соответственно площадью Аsp,tot и As,tot;

ξcir — относительная площадь сжатой зоны бетона, определяемая по формуле

,        (123)

здесь ; ωs = ηr ;

ηr = 1,1 — для арматуры с условным пределом текучести (см. п. 2.16);

ηr = 1,0 — для арматуры с физическим пределом текучести;

δsp(s) = 1,5 + 6Rs ⋅ 10-4 (Rs - в МПа);

σsp — предварительное напряжение с учетом коэффициента γsp, большего единицы;

zsp, zs — расстояния от равнодействующей их соответственно в напрягаемой и ненапрягаемой арматуре растянутой зоны до центра тяжести сечения, определяемые по формуле

       zsp(s) = (0,2 + 1,3 ξcir) rsp(s) ,        (124)

но принимаемые не более zsp(s);

φsp, φs — коэффициенты, принимаемые равными:

       φsp(s) = ωp(s) (1 - δsp(s) ξcir) ;        (125)

если φsp ≤ 0 или φs ≤ 0, значение ξcir снова вычисляется по формуле (123), при этом соответственно принимается Аsp = 0 либо As = 0.

Если ξcir < 0,15, в условие (122) подставляется значение ξcir, определяемое по формуле

        ,        (126)

при этом значения φsp, φs, zsp и zs определяются по формулам (125) и (124) при ξcir = 0,15.

Эксцентриситет силы N относительно центра тяжести сечения e0 определяется с учетом прогиба элемента согласно пп. 3.39 и 3.40.

Примеры расчета

Прямоугольные сечения

Пример 18. Дано: колонна с размерами сечения — b = 400 мм, h = 700 мм, aр = as = a's = a′p = 40 мм; бетон класса В30 (Rb = 19 МПа при γb2 = 1,1, Еb = 2,9 • 104 МПа); арматура симметричная класса A-V (Rs = 680 МПа, Еs = 1,9 • 105 МПа), площадью сечения: напрягаемая — Asp = 402 мм2 (2 ∅ 16), ненапрягаемая - As = 201 мм2 (1 ∅ 16); предварительное напряжение с учетом всех потерь σsp = 575 МПа; натяжение арматуры электротермическое неавтоматизированное; площадь приведенного сечения Аred = 287 600 мм2; усилие предварительного обжатия с учетом всех потерь напряжений при γsp = 0,9 Р = 397 кН; продольные силы от постоянных и длительных нагрузок Nl = 1890 кН, от всех нагрузок N = 2450 кН; изгибающий момент от кратковременных нагрузок, полученный из статического расчета по недеформированной схеме, М = Мsh = 245 кН⋅м; расчетная длина l0 = 14,6 м.

Требуется проверить прочность сечения.

Р а с ч е т. h0 = 700 - 40 = 660 мм. Так как l0/h = 14,6/0,7 = 20,8 > 10, расчет ведем с учетом прогиба колонны согласно п. 3.39, вычисляя Ncr по формуле (104).

Для этого определяем φl по формуле (105), принимая по табл. 30 β = 1,0:

= 1,583;

0,1 м = 100 мм > ea = = 23 мм (см. п. 3.35);

= 0,143 > δe,min = 0,5 - 0,01 - 0,01 Rb =

= 0,5 - 0,01 ⋅ 20,8 - 0,01 ⋅ 19 = 0,102 .

Следовательно, принимаем δe = e0/h = 0,143.

Напряжение обжатия в бетоне равно:

σbp = Р/Аred = 397 000 / 287 600 = 1,38 МПа.

Поскольку е0/h < 1,5, в формуле (107) оставляем e0/h = 0,143.

Тогда        φp = 1 + 12 0,143 = 1,125 .

Моменты инерции бетонного сечения и арматуры равны:

= 11430 ⋅ 106 мм4 ;

2 ⋅ 603 ⋅ 3102 = 116 ⋅ 106 мм4 ;

6,55 ;

=

= 4335 кН.

Коэффициент η определяем по формуле (103):

= 2,3 .

Значение e равно:

е = е0 η + = 100 ⋅ 2,3 + 310 = 540 мм.

Проверку прочности ведем согласно п. 3.41.

Поскольку в сечении применяется ненапрягаемая арматура класса A-V с условным пределом текучести, то, согласно п. 3.41 и примечанию к п. 3.3, значение Asp = А′sp заменяем на Asp1 = А'sp1 = Аsp + As = 603 мм2, a напряжение σsp2 заменяем на усредненное напряжение σsp,m и принимаем Аs = А's = 0:

= 383 МПа.

Определяем напряжение в арматуре σsc согласно п. 3.8, принимая σsc,u = 400 МПа, а σsp,m с учетом коэффициента γsp = 1,1:

σsc = σsc,u - σsp,m = 400 - 1,1 ⋅ 383 = -20 МПа.

Относительную высоту сжатой зоны бетона при γs6 = 1 вычисляем по формуле (108):

= 0,572 .

Из табл. 26 при γb2 = 1,1, классе арматуры A-V, классе бетона В30 и = 0,507 находим значение ξR = 0,42.

Поскольку ξ1 = 0,572 > ξR = 0,42, а арматура класса A-V с условным пределом текучести, высоту сжатой зоны определяем по формуле (111). Так как натяжение электротермическое неавтоматизированное, принимаем β = 0,8, а значение ξel находим из табл. 31. При классе арматуры A-V, классе бетона В30 и σsp/Rs = 0,507 ξel = 0,59.

Тогда        

= 369 мм .

Поскольку x = 369 мм < ξelh0 = 0,59 • 660 = 389 мм, оставляем x = 369 мм.

Прочность проверяем из условия (109):

Rb bx(h0 - 0,5x) + σscA′sp1 (h0 - a′p) = 19 ⋅ 400 ⋅ 369 (660 - 0,5 ⋅ 369) -

- 20 ⋅ 603 (660 - 40) = 1326 ⋅ 106 H⋅мм > Ne = 2450 ⋅ 103 ⋅ 540 =

= 1323 ⋅ 106 H⋅мм,

т. е. прочность сечения обеспечена.

Кольцевые сечения

Пример 19. Дано: внутренний радиус r1 = 150 мм, наружный радиус r2 = 250 мм; бетон класса В30 (Rb = 19 МПа при γb2 = 1,1, Еb = 2,9 • 104 МПа); напрягаемая арматура класса A-IV (Rs = 510 МПа, Rsc = 400 МПа, Es = 1,9⋅105 МПа), площадью сечения Аsp,tot = 1470 мм2 (13 ∅ 12) распределена равномерно посередине толщины кольца; предварительное напряжение с учетом всех потерь σsp2 = 350 МПа; продольная сила от постоянных и длительных нагрузок N = Nl = 250 кН; изгибающий момент от ветровой нагрузки M = Мsh = 120 кН⋅м; расчетная длина элемента l0 = 6 м.

Требуется проверить прочность сечения.

Р а с ч е т. Вычисляем площадь кольцевого сечения:

А = π (r22 - r12) = 3,14(2502 - 1502) = 125600 мм2 ;

= 6,55 ;

Ared = A + αAsp,tot = 125 600 + 6,55 • 1470 = 136 900 мм2.

Радиус инерции сечения

= 146 мм.

Тогда гибкость элемента l0/i = 6000 / 146 = 41 > 35.

Следовательно, расчет ведем с учетом прогиба элемента согласно п. 3.39, вычисляя Ncr по формуле (104). Для этого определяем:

rsp = rm = = 200 мм = 0,2 м ;

= 1,294 ;

= 0,48 м = 480 мм > 16,7 мм (см. п.3.35).

Так как = 0,96 > δe,min = 0,5 - 0,01 - 0,01 Rb , принимаем δe = е0/D = 0,96.

Напряжение обжатия в бетоне при γsp = 0,9 равно:

= 3,4 МПа .

Поскольку е0/D < 1,5, в формуле (107) оставляем е0/D = 0,96. Тогда

= 3,06 .

Моменты инерции бетонного сечения и арматуры равны:

2670 ⋅ 106 мм4 ;

29,4 ⋅ 106 мм4 ;

=

=

= 4885000 Н = 4885 кН.

Коэффициент η равен:

= 1,05 .

Проверку прочности производим согласно п. 3.43.

Определяем значение ξcir по формуле (123), принимая Аs,tot = 0 и γsp = 1,1. Для этого вычисляем:

δsp = 1,5 + 6Rs ⋅ 10-4 = 1,5 + 6 ⋅ 510 ⋅ 10-4 = 1,8 ;

σsp = 1,1 ⋅ 350 = 375 МПа;      ηr = 1,1;

= 0,36 ;

=

= 0,31 > 0,15 .

Следовательно, значение ξcir оставляем без изменения. Значение φsp равно:

φsp = ωp (1 - δsp ξsir) = 0,36(1 - 1,8 ⋅ 0,31) = 0,16.

Так как φsp > 0, значение оставляем без изменения. Значение zsp равно:

zsp = (0,2 + 1,3 ξcir)rsp = (0,2 + 1,3 ⋅ 0,31)200 = 120,6 мм.

Проверяем условие (122), принимая эксцентриситет е0 с учетом η:

(Rb Arm + RscAsp,totrsp) + Rs Asp,tot φsp zsp =

=(19⋅125600⋅200 + 400⋅1470⋅200) ⋅ 1470 ⋅ 0,16 ⋅ 120,6 =

= 171 ⋅ 106 Н⋅мм = 171 кН⋅м > Ne0η = Mη = 120 ⋅ 1,05 = 126 кН⋅м ,

т.е. прочность сечения обеспечена.

Расчет элементов на воздействие предварительного обжатия

3.44. При расчете элемента на воздействие предварительного обжатия с учетом нагрузок, действующих в стадии изготовления, усилие в напрягаемой арматуре Np вкодится в расчет как внешняя нагрузка. Это усилие определяется следующим образом:

а) при натяжении арматуры на упоры

Np = (σsp1 - 330) A′sp ,

где A'sp — площадь сечения напрягаемой арматуры, расположенной в зоне предполагаемого разрушения бетона от сжатия в стадии изготовления;

σsp1 — определяется при коэффициенте γsp, большем единицы, МПа;

б) при натяжении арматуры на бетон усилие Np определяется от всей напрягаемой арматуры, при этом напряжения в ней принимаются равными:

если вся арматура натягивается одновременно — σcon2, где σcon2 -  контролируемые напряжения в арматуре (см. п. 1.23);

если арматура натягивается поочередно группами —  σsp1 - σsc,p ,

где         ,        (127)

но не более 280 МПа;

здесь Amin, Аmax — соответственно наименьшая и наибольшая площади поперечных сечений обжимаемого элемента;

Аsp, Аsp,n — площади сечения соответственно всех групп и последней группы напрягаемой арматуры.

Расчет в общем случае производится согласно указаниям п. 3.18, при этом в правую часть уравнения (61) добавляется значение Nр, значение М в условии (60) принимается равным моменту усилия Np относительно оси, параллельной прямой, ограничивающей сжатую зону и проходящей через центр тяжести сечения наиболее растянутого (или наименее сжатого) стержня, а площади сечения стержней, которые были использованы для определения усилия Np, в расчете не учитываются.

При расположении усилия Np в плоскости симметрии сечения и при арматуре, сосредоточенной у наиболее и у наименее обжатых граней, расчет прочности на действие предварительного обжатия может производиться согласно пп. 3.46—3.48, где принимается Asp = 0, если арматура натягивается на бетон. При наличии ненапрягаемой арматуры с условным пределом текучести следует учитывать примечание к п. 3.3.

При расчете прочности на обжатие расчетное сопротивление бетона сжатию Rb = Rb(p) определяется по табл. 13 при классе бетона, равном его передаточной прочности Rbp, и γb2 = 1; при этом следует учитывать коэффициент γb8 (см. табл. 14, поз. 5). Кроме того, значение σsc,u в формулах (64) и (21) принимается равным 330 МПа.

При натяжении арматуры на упоры расчет элементов на действие центрального обжатия может не производиться.

3.45. При натяжении арматуры на упоры влияние прогиба элемента не учитывается. Также не учитывается влияние прогиба элемента при натяжении на бетон арматуры, расположенной в закрытых каналах и не смещаемой по поперечному сечению при прогибе элемента.

При натяжении на бетон арматуры, расположенной в каналах, пазах, выемках или за пределами сечения, не имеющей сцепления с бетоном и способной смещаться по поперечному сечению элемента, влияние прогиба элемента должно быть учтено, согласно указаниям п. 3.39, как для ненапрягаемого элемента. При этом расчетная длина принимается равной расстоянию между устройствами, прикрепляющими арматуру к бетону по длине элемента, а в значении Is учитывается только ненапрягаемая арматура.

3.46. Для элементов прямоугольного и таврового сечений с полкой в менее обжатой зоне (черт. 29) расчет прочности на действие предварительного обжатия производится в зависимости от высоты сжатой зоны

;

а) при ξ = х / h0 ≤ ξR [см. формулу (21) при σsc,u = 330 МПа] - из условия

       Npe ≤ Rb(p) bx (h0 - 0,5х) + Rsc A's (h0 - a′s),        (128)

где е - см. п. 3.48;

б) при ξ > ξR — из условия

       Npe ≤ αR Rb(p) bh02 + Rsc A′s (h0 - a′s) ,        (129)

где αR = ξR (1 - 0,5ξR).

Значения ξR и αR при ненапрягаемой арматуре менее обжатой зоны классов А-III и Вр-I можно определять по табл. 33.

Черт. 29. Схема усилий в поперечном сечении внецентренно обжатого железобетонного элемента с прямоугольной сжатой зоной

Таблица 33

ω = α - 0,008 Rb(p) ; ; ; αR = ξR (1 -ξR/2).

Если ξ > ξR, расчетную несущую способность на действие обжатия при необходимости можно несколько увеличить, используя условие (128) при значении х, определяемом следующим образом:

при отсутствии в менее обжатой зоне арматуры с условным пределом текучести

        ,        (130)

где         ;

, ω — см. табл. 33;

при наличии в менее обжатой зоне арматуры с условным пределом текучести

,        (131)

где ξel — см. п 3.41в при σsc,u = 330 МПа;

β — см. п. 3.18.

При этом, если значение х, определенное по формуле (131), оказывается больше ξelh0, то в условие (128) подставляется значение х, определяемое по формуле (130), где и ω находят по табл. 33.

Значение е в условиях (128) и (129) определяется согласно п. 3.48.

3.47. Для элементов двутаврового и таврового сечений с полкой в более обжатой зоне (черт. 30) расчет прочности на действие предварительного обжатия производится следующим образом:

если соблюдается условие

       Np ≤ Rb(p) b'f h'f - Rs Asp - Rs As + Rsc A's        (132)

(т.е. граница сжатой зоны проходит в полке), расчет производится как при отсутствии полки в более обжатой зоне в соответствии с п. 3.46 при b = b'f ;

Черт. 30. Схема усилий в поперечном сечении внецентренно обжатого железобетонного элемента с полкой в сжатой зоне

если условие (132) не соблюдается (т.е. граница сжатой зоны проходит в ребре), расчет производится в зависимости от высоты сжатой зоны

,

а) при [см. формулу (21) п. 3.6 при σsc,u = 330 МПа] - из условия

Npe ≤ Rb(p) bx (h0 - 0,5x) + Rb(p) Aoν (h0 - 0,5h′f) + Rsc A's (h0 - a′s),     (133)

где e - см. п. 3.48;

б) при ξ > ξR - из условия

       Npe ≤ αR Rb(p) bh02 + Rb(p) Aoν (h0 - 0,5h′f) + Rsc A's (h0 - a′s),            (134)

где αR = (1 - 0,5ξR);

Aoν= (b′f - b)h′f  — площадь сечения сжатых свесов.

Значения ξR и αR при ненапрягаемой арматуре менее обжатой зоны классов А-III и Вр-I можно определять по табл. 33.

Если ξ > ξR , расчетную несущую способность на действие обжатия при необходимости можно несколько увеличить, используя условие (133) при значении х, определенном по формулам (130) или (131), в которых сила Np уменьшается на величину Rb(p) Аoν.

3.48. Значение е в условиях. (128), (129), (133) и (134) определяется по формулам:

при натяжении на упоры

                ;        (135)

при натяжении на бетон

               .        (136)        

В формулах (135) и (136):

М — момент от нагрузок, действующих в стадии изготовления; знак «плюс» принимается, если момент усилия Np относительно арматуры S и момент М совпадают по направлению, знак «минус» — если направления этих моментов противоположны;

t0p — эксцентриситет силы Np относительно центра тяжести приведенного сечения;

η — см. пп. 3.39 и 3.45;

у — расстояние от центра тяжести приведенного сечения до наиболее обжатой грани.

Значение в формуле (136) принимается не менее ea (см. п. 3.35).

Примеры расчета

Пример 20. Дано: ребристая плита покрытия длиной 12 м с поперечным сечением ребра по черт. 31; напрягаемая арматура из канатов класса К-7 натягивается на упоры; предварительное напряжение с учетом первых потерь при γsp > l σsp1 = 900 МПа; передаточная прочность тяжелого бетона Rbp = 25 МПа; масса плиты 7,4 т; монтажные петли расположены на расстоянии 800 мм от торца плиты.

Требуется проверить прочность плиты в стадии изготовления.

Черт. 31. К примеру расчета 20

Р а с ч е т. Из черт. 31 видно, что в наиболее обжатой зоне располагается напрягаемая арматура класса К-7, площадью А′sp = 566 мм2 (4 ∅ 15). Heнапрягаемую арматуру 1 ∅ 5 класса Вр-I, расположенную в этой зоне, в расчете не учитываем, поскольку она не удовлетворяет конструктивным требованиям п. 5.39.

В менее обжатой зоне располагается ненапрягаемая арматура с физическим пределом текучести 1 ∅ 10 классов А-III (Аs1 = 78,5 мм2) и 1 ∅ 5 Вр-I +7 ∅ 4 Вр-I (Аs2 = 19,6 + 87,9 = 107,6 мм2).

Поскольку значения Rs для арматуры классов А-III и Вр-I (∅4 и ∅5) близки, принимаем точку приложения равнодействующей усилий в арматуре менее обжатой зоны в центре тяжести сечения этой арматуры, и тогда расстояние ее от верхней грани сечения равно:

31,6 мм .

Следовательно, h0 = h - а = 450 - 31,6 = 418 мм.

Из черт. 31 имеем = 55.

Расчетное усилие обжатия, согласно п. 3.44, равно:

Np = (σsp1 - 330)А'sp = (900 - 330) 566 = 322 600 Н = 322,6 кН.

Определяем значение е согласно п. 3.48. Равномерно распределенная нагрузка от собственного веса плиты, учитывая указания п. 2.14 и коэффициент надежности по нагрузке γf = 1,1, будет равна:

6,8 кН/м.

Поскольку монтажные петли располагаются на расстоянии l = 0,8 м от торца, невыгоднейший момент от собственного веса, растягивающий верхнюю грань, будет возникать при подъеме плиты. Определим этот момент с учетом коэффициента 1,4 (см. п. 1.9) для половины сечения плиты:

= 1,52 кН⋅м.

Тогда        e = h0 - a′p + 368 мм.

Расчетное сопротивление бетона, соответствующее передаточной прочности Rbp = 25 МПа согласно табл. 13 при γb2 = 1, равно Rb(p) = 14,5 МПа, а с учетом коэффициента γs8 = 1,1 (см. табл. 14, поз. 5) - Rb(p) = 1,1⋅14,5 = 16 МПа.

Поскольку ширина ребра b переменна, принимаем в первом приближении ширину ребра посередине высоты сжатой зоны равной ξRh0. Из табл. 33 при Rbp = 25 МПа, тяжелом бетоне и проволочной напрягаемой арматуре находим ξR = 0,52. Тогда

= 114,2 мм .

Высота сжатой зоны при Аsp = 0 и А's = 0 равна:

= 214,2 мм.

Поскольку ξ = x/h0 = 214,2 / 418 = 0,512 < ξR = 0,52, прочность проверяем из условия (128). При этом ширину ребра не пересчитываем, так как полученное значение ξ близко к ξR:

Rb(p) bx (h0 - 0,5х) = 16 ⋅ 114,2 ⋅ 214,2 (418 - 0,5 ⋅ 214,2) =

= 121,7 ⋅ 106 Н⋅мм = 121,7 кН⋅м > Np e = 322,6 ⋅ 0,368 = 118,7 кН⋅м,

т.е. прочность в стадии изготовления обеспечена.

Центрально-растянутые элементы

3.49 (3.26). При расчете сечений центрально-растянутых железобетонных элементов должно соблюдаться условие

       N ≤ η Rs Asp,tot + Rs As,tot ,        (137)

где η — см. п. 3.7;

Asp,tot, As,tot — площади сечения всей продольной соответственно напрягаемой и ненапрягаемой арматуры.

Внецентренно растянутые элементы

РАСЧЕТ ЭЛЕМЕНТОВ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
ПРИ РАСПОЛОЖЕНИИ ПРОДОЛЬНОЙ СИЛЫ
В ПЛОСКОСТИ СИММЕТРИИ

3.50 (3.27). Расчет прямоугольных сечений внецентренно растянутых элементов с арматурой, сосредоточенной у наиболее растянутой и у сжатой (наименее растянутой) граней, должен производиться в зависимости от положения продольной силы N:

а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S' (черт. 32, а), т.е. при е' ≤ h0 — а′, - из условий:

       Ne' ≤ (ηRsAsp + RsAs) (h0 - а′);        (138)

       Ne ≤ (ηRsA′sp + RsA′s) (h0 - а′) ,        (139)

где η —см. п. 3.7;

при симметричной арматуре используется только условие (138);

б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S' (черт. 32, б), т.е. при е' > h0 - а′, - из условия

Ne ≤ Rb bx(h0 - 0,5x) + Rsc A's (h0 - а′s) + σsc A′sp (h0 - a′p ) ,        (140)

при этом высота сжатой зоны х определяется по формуле

,        (141)

где γs6 - см. формулу (23); при этом допускается определять из формулы (141) без учета γs6;

σsc — см. п. 3.8.

Черт. 32. Схема усилий в прямоугольном сечении внецентренно
растянутого железобетонного элемента при расчете его на прочность

а — продольная сила N приложена между равнодействующими усилий
в арматуре S и S'; б — то же, за пределами расстояния между
равнодействующими усилий в арматуре S и S'

Если полученное из расчета по формуле (141) значение х > ξRh0, в условие (140) подставляется х = ξRh0, где определяется согласно п. 3.6.

Если х < 0, прочность сечения проверяется из условия (138).

При применении ненапрягаемой арматуры с условным пределом текучести следует учитывать примечание к п. 3.3.

П р и м е ч а н и е. Если при е' > h0 - а' высота сжатой зоны, определенная без учета ненапрягаемой арматуры S',

меньше 2a′s, расчетную несущую способность можно несколько увеличить, произведя расчет по формулам (140) и (141) без учета ненапрягаемой арматуры S'.

3.51. Элементы прямоугольного сечения с симметричной арматурой, расположенной в несколько рядов по высоте сечения, рассчитываются при силе N, приложенной между крайними рядами арматуры, из условия

       Ne1 ≤ η Rs Ssp + Rs Ss ,        (142)

где e1 — расстояние от силы N до оси, перпендикулярной направлению эксцентриситета и проходящей через наименее растянутый ряд арматуры;

Ssp, Ss — статические моменты площади сечения соответственно всей напрягаемой и всей ненапрягаемой арматуры относительно той же оси;

η — см. п. 3.7.

Если сила N приложена за пределами расстояния между крайними рядами арматуры, расчет производится по формулам общего случая согласно п. 3.53.

3.52. Определение требуемого количества продольной арматуры производится следующим образом:

а) при e' ≤ h0 - а' площадь сечения напрягаемой арматуры S и S′ определяется соответственно по формулам:

;        (143)

;        (144)

б) при e' > h0 - а' площадь сечения напрягаемой арматуры S определяется по формуле

        ,        (145)

где ξ определяется по табл. 28 в зависимости от значения

        ;        (146)

γs6 — см. п. 3.7.

При этом должно соблюдаться условие αm ≤ αR = ξR (1 - ξR/2) (ξR — см. табл. 26 или 27). В противном случае следует увеличить площадь сечения ненапрягаемой арматуры A's, повысить класс бетона или увеличить размеры сечения.

Если αm < 0, площадь сечения напрягаемой арматуры S определяется по формуле (143).

При подборе симметричной напрягаемой арматуры в первом приближении в формулах (145) и (146) принимается A′sp = 0. При этом, если напряжение σsc сжимающее (т.e. σsc > 0), повторный расчет можно не производить.

П р и м е ч а н и е. При e' > h0 - a' и при отсутствии напрягаемой арматуры S' необходимое количество напрягаемой арматуры S можно несколько снизить, если значение ξ, определенное по табл. 28 без учета ненапрягаемой арматуры S', т. e. по значению , оказывается меньше 2a's/h0. В этом случае площадь сечения напрягаемой арматуры S определяется по формуле

        ,        (147)

где значение ζ и значение ξ, необходимое для вычисления γs6, определяются по табл. 28 в зависимости от .

Общий случай расчета нормальных сечений
внецентренно растянутого элемента
(при любых сечениях, внешних усилиях и любом армировании)

3.53. Расчет нормальных сечений внецентренно растянутого элемента в общем случае (черт. 33) должен производиться из условия

       Ne' ≤ Σ σsi Ssi - Rb Sb ,        (148)

где e' — расстояние от продольной силы N до оси, параллельной прямой, ограничивающей сжатую зону и проходящей через точку сжатой зоны, наиболее удаленную от указанной прямой;

σsi — напряжение в 1-м стержне продольной арматуры;

Ssi — статический момент площади сечения i-го стержня продольной арматуры относительно указанной оси;

Sb — статический момент площади сечения сжатой зоны бетона относительно указанной оси.

Черт. 33. Общий случай расчета внецентренно растянутого элемента

I — точка приложения растягивающей силы N; А — точка приложения равнодействующей усилий в арматуре и бетоне сжатой зоны; Б — точка приложения равнодействующей усилий в арматуре растянутой зоны;
1-6 — арматурные стержни

Высота сжатой зоны бетона х и напряжения σsi определяются из совместного решения уравнений (61)—(64) с добавлением в левую часть формулы (61) значения N.

При косом внецентренном растяжении для определения положения границы сжатой зоны кроме использования формул (61)—(64) требуется соблюдение дополнительного условия, что точки приложения внешней продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и равнодействующей усилий в растянутой арматуре должны лежать на одной прямой.

Расчет сечений, наклонных к продольной оси элемента

3.54. Расчет наклонных сечений внецентренно растянутых элементов на действие поперечной силы производится как для изгибаемых элементов согласно пп. 3.19-3.30; при этом в случаях, когда N < Р, значение Р в формуле (75) уменьшается на значение продольной силы N, а в случаях, когда N > Р, формула (75) заменяется формулой

                ,        (149)

при этом значение φn принимается по абсолютной величине не более 0,8. Здесь Р — усилие от предварительного напряжения в арматуре, расположенной в растянутой зоне; при расположении силы N между крайними рядами арматуры учитывается усилие от всей напрягаемой арматуры, кроме арматуры наименее растянутого ряда. В этом случае рабочая высота сечения h0 отсчитывается от наиболее растянутого ряда.

Расчет наклонных сечений внецентренно растянутых элементов на действие изгибающего момента производится как для изгибаемых элементов согласно пп. 3.31-3.34. При этом высота сжатой зоны в наклонном сечения определяется с учетом растягивающей силы N по формуле (141) или согласно п. 3.53.

Примеры расчета

Внецентренно растянутые элементы

Пример 21. Дано: размеры сечения нижнего пояса безраскосной фермы — b = 220 мм, h = 240 мм, a = a' = 40 мм; бетон класса В30; продольная напрягаемая арматура симметричная класса A-IV (Rs = 510 МПа, η = 1,2), площадью сечения Asp = А′sp = 763 мм2 (3 ∅ 18); продольная растягивающая сила N = 600 кН; максимальный изгибающий момент М = 24 кН•м.

Требуется проверить прочность нормального сечения.

Р а с ч е т.   h0 = h - а = 240 - 40 = 200 мм;

= 0,04 м = 40 мм ;

е′ = е0 + 40 = 120 мм .

Так как e' = 120 мм < h0 - a' = 200 - 40 = 160 мм, прочность сечения проверяем из условия (138). Условие (139) не проверяем, поскольку арматура симметричная:

η Rs Asp (h0 - a′p) = 1,2 ⋅ 510 ⋅ 763 (200 - 40) = 74,7 ⋅ 106 H⋅мм =

= 74,7 кН⋅м > Ne′ = 600 ⋅ 0,12 = 72 кН⋅м,

т.e. прочность сечения обеспечена.

Пример 22. Дано: П-образная плита перекрытия; к нижней грани ее продольного ребра приложена растягивающая сила N = 66 кН, вызванная сдвигающими усилиями в диске перекрытия от ветровых нагрузок; размеры поперечного сечения плиты (для половины сечения) — h = 400 мм, b = 85 мм, b'f = 350 мм, h'f = 50 мм, а = 37 мм; бетон класса В25 (Rb = 19 МПа при γb2 = 1,1); продольная растянутая арматура напрягаемая класса A-V (Rs = 680 МПа) и ненапрягаемая класса А-III (Rs = 365 МПа); площади сечения арматуры Аsp = 314 мм2 (1 ∅ 20) и Аs = 785 мм2 (1 ∅ 10).

Требуется проверить прочность нормального сечения плиты.

Р а с ч е т.  h0 = h — а = 400 — 37 = 363 мм. Поскольку сила приложена за пределами расстояния между арматурой S и S', прочность сечения проверяем согласно п. 3.50б.

Предполагая, что граница сжатой зоны проходит в полке, расчет ведем как для прямоугольного сечения (по аналогии с изгибаемыми элементами), принимая b = b'f = 350 мм. При этом, если х < h′f, т.е. = 0,138, то ξ меньше 0,5 ξR (см. табл. 26) и, следовательно, согласно п. 3.7, можно принять γs6 = η = 1,15.

По формуле (141) определим высоту сжатой зоны х:

=

= 31,3 мм < h′f=50 мм ,

т.e. граница сжатой зоны действительно проходит в полке.

Определим Ne - момент внешних сил относительно точки приложения равнодействующей усилий в арматуре S:

Ne=Na + М=66 ⋅ 0,037 + 69=71,44 кН⋅м.

Прочность сечения проверяем из условия (140):

Rb bx (h0 - 0,5х)=19 ⋅ 350 ⋅ 31,3(363 - 0,5 ⋅ 31,3)=72,3 ⋅ 106 H⋅мм=
=72,3 кН⋅м > Ne=71,44 кН⋅м,

т.е. прочность сечения обеспечена.

Пример 23. Дано: размеры сечения — b=240 мм, h=360 мм; расположение продольной напрягаемой арматуры класса A-V (Rs=680 МПа) — по черт. 34; центрально-приложенная растягивающая сила N=1000 кН; изгибающий момент М=80 кН⋅м; площадь сечения всей продольной арматуры Asp,tot=2513 мм2 (8 ∅ 20).

Черт. 34. К примеру расчета 23

1 - центр тяжести сечения

Требуется проверить прочность нормального сечения.

Р а с ч е т. Расстояние от крайнего ряда арматуры до центра тяжести сечения, согласно черт. 34, равно:

120 мм .

Поскольку e0=M / N=80 / 1000=0,08 м=80 мм < a1=120 мм, сила N приложена между крайними рядами арматуры и прочность сечения можно проверить из условия (142).

Статический момент площади сечения всей арматуры относительно крайнего ряда арматуры равен:

Ssp=Аsp,tot a1=2513 • 120=301600 мм3 .

Расстояние от силы N до наименее растянутого ряда арматуры e1=  e0 + a1=80 + 120=200 мм.

Согласно п. 3.7, η=1,15 (для арматуры класса A-V);

η Rs Ssp=1,15 ⋅ 680 ⋅ 301 600=235,85 ⋅ 106 H⋅мм=
=235,85 кН⋅м > Ne1=1000 ⋅ 0,2=200 кН⋅м,

т. е. прочность сечения обеспечена.

Пример 24. Дано: размеры сечения нижнего пояса подстропильной фермы — b=550 мм, h=210 мм, а=а'=50 мм; продольная напрягаемая арматура в виде канатов класса К-7, диаметром 15 мм (Rs=1080 МПа); продольная растягивающая сила N=2200 кН⋅м; изгибающий момент М=44 кН⋅м.

Требуется определить площадь сечения симметричной продольной арматуры.

Р а с ч е т.  h0=h - a=210 - 50=160 мм;

e0=M / N=44 / 2200=0,02 м=20 мм;

е'=e0 + h / 2 - a=20 + 210 / 2 - 50=75 мм.

Так как h0 - a'=160 - 50=110 мм > е'=75 мм, площадь сечения арматуры S и S′ определяем по формуле (143), принимая η=1,15:

1208 мм2.

Принимаем Asp=А'sp=1273 мм2 (9 ∅ 15 К-7).

Пример 25. Дано: размеры сечения нижнего пояса безраскосной фермы — b=240 мм, h=360 мм, а=а'=60 мм; бетон класса В30 (Rb=15,5 МПа при γb2=0,9); продольная напрягаемая арматура класса A-V (Rs=680 МПа); растягивающая сила N=480 кН; изгибающий момент М=72 кН⋅м.

Требуется определить площадь сечения симметричной продольной арматуры.

Р а с ч е т. h0=h - а=360 - 60=300 мм; е0=M / N=72 / 480=0,15 м=150 мм;

е'=е0 + h/2 - а′=150 + 360 / 2 - 60=270 мм;

е=е0 - h/2 + а=150 - 360/2 + 60=30 мм.

Так как h0 - а′=300 — 60=240 мм < е'=270 мм, арматуру подбираем согласно п. 3.52б.

Тогда по формуле (145) определяем значение αm, принимая в первом приближении A'sp=0:

=0,043 .

Из табл. 28 для αm=0,043 находим ξ=0,045.

Из табл. 26 при γb2=0,9, классе арматуры A-V, классе бетона В30 и (σsp + Δσsp)/Rs=0,6 (см. примечание к табл. 26) находим ξR=0,5.

Так как ξ=0,045 < 0,5 ξR=0,25, принимаем γs6=η=1,15.

Площадь сечения арматуры S определяем по формуле (145):

678 мм2 .

При σ′sp=γsp0,6Rs=1,1 ⋅ 0,6 ⋅ 680=449 МПа значение σsc=σsc,u -σ′sp=500 — 449 > 0, следовательно, повторный расчет не производим.

Принимаем Аsp=А′sp=760 мм2 (2 ∅ 22).

Пример 26. Дано: элемент нижнего пояса безраскосной фермы с размерами сечения — b=220 мм, h=240 мм, a=а′=40 мм; длина элемента в свету между стойками 2,8 м; бетон тяжелый класса В30 (Rbt=1,1 МПа при γb2=0,9); поперечная арматура — в виде согнутых сеток из проволоки класса Bp-I (Rsw=260 МПа при d=5 мм); продольная центрально-приложенная растягивающая сила N=300 кН; усилие обжатия от симметрично расположенной в два ряда напрягаемой арматуры Р=480 кН; поперечная сила, постоянная по длине элемента, Q=17 кН; максимальный изгибающий момент в сечении у конца элемента Mmax=23,8 кН•м; характеристики приведенного сечения: Ared=58100 мм2, Ired=286,7 • 106 мм4.

Требуется определить диаметр и шаг поперечных стержней (хомутов).

Р а с ч е т.   h0=h - a=240 - 40=200 мм.

Согласно п. 3.54, определим коэффициент φn. Поскольку напрягаемая арматура расположена в два ряда и симметрично относительно центра тяжести сечения, в значении P учитываем усилие только от половины напрягаемой арматуры, т.е. Р=0,5 • 480=240 кН.

Так как Р=240 кН < N=400 кН, φn определяем по формуле (149):

=-0.661 .

Поскольку |φn|=0,661 < 0,8, оставляем φn=-0,661.

Согласно п. 3.19, выясним, требуются ли хомуты из условия прочности. Для этого проверим условие (93) при длине проекции наклонного сечения с, равной длине участка, где образуются нормальные трещины, т.е. при с=, где Mcrc1 — внешний изгибающий момент, соответствующий образованию трещин.

Определим момент Мcrc1 из условия (190), представив его в виде равенства

Мr=Мcrc1 + Nr=Мcrc=Rbt Wpl + Р (e0p + r),

откуда при e0p=0 имеем

Mcrc1=Rbt Wpl + (P - N)r (здесь Р - полное усилие обжатая).

Согласно пп. 4.2 и 4.3, определяем Wpl и r:

=120 мм ; =239⋅106 мм3 ;

Wpl=γ Wred=1,75 • 239 • 106=4,18 • 106 мм3 (здесь у=1,75; см. табл. 39).

Принимая в целях упрощения расчета φ=0,8, имеем

=32,9 мм .

Следовательно, Мcrc1=1,1 • 4,18 • 106 + (480 - 400) 103 • 32,9=
=7,23 • 106 H⋅мм=7,23 кН⋅м;

=0,975 м .

Поскольку с=975 мм > 2,5 h0=2,5 • 200=500 мм, согласно п. 3.30,

Qb1=Qb.min=  φb3 (1+φn)Rbtbh0=0,6( -0,661)1,1⋅220⋅200=9845 H=95 кН,

где φb3=0,6 (см. табл. 29).

Qb1=9,85 кН < Q=17 кН, т.е. условие (94) не выполняется, и хомуты подбираем из расчета по прочности согласно п. 3.23а.

По формуле (73) определяем Мb, принимая φb2=2 (см. табл. 29) и φf=0:

Mb=φb2 (1+φn) Rbt bh02=2(1 - 0,661)1,1⋅220⋅2002=6,56 ⋅ 106 H⋅мм.

Поскольку поперечная сила не изменяется по длине элемента, принимаем длину проекции с равной длине элемента, т.е. с=2,8 м.

Qb=Mb/с=6,56/2,8=2,34 кН < Qb,min=9,85 кН.

Принимаем Qb=Qb, min=9,85 кН.

Поскольку с=2,8 м > 2/h0=2 • 0,2=0,4 м, то co=2h0=0,4 м.

Тогда =1 .

Так как х==0,727 < x0 , значение qsw определяем по формуле (79) :

=21,25 кН/м .

Максимально допустимый шаг хомутов, согласно п. 3.21, равен:

=

=289 мм > =40 мм .

Принимаем шаг хомутов s=200мм < 2b=440 мм (см. п. 5.38).

Тогда        =16,3 мм2 .

Принимаем два хомута диаметром по 4 мм (Аsw=21,1 мм2).

Элементы, работающие на кручение с изгибом

3.55. Расчет элементов, работающих на кручение с изгибом, производится согласно пп. 3.82—3.92 «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры». При этом напрягаемая арматура учитывается в расчете аналогично ненапрягаемой со своим расчетным сопротивлением без учета коэффициента γs6, а ссылки на другие разделы указанного Пособия заменяются ссылками на соответствующие разделы настоящего Пособия (определение ξR по п. 3.6, расчет нормальных сечений по пп. 3.22—3.30, определение значения Mu по п. 3.43).

РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
НА ВЫНОСЛИВОСТЬ

3.56. Расчет железобетонных конструкций на выносливость производится при воздействии многократно повторяющейся (подвижной или пульсирующей) нагрузки, вызывающей значительный перепад напряжений в бетоне или растянутой арматуре, если число повторений нагрузки за период эксплуатации здания или сооружения достаточно велико (порядка 105 и более).

Таким нагрузкам подвергаются подкрановые балки, эстакады, шпалы, перекрытия под неуравновешенные машины (например, вентиляторы, центрифуги) и т. п.

Подкрановые балки при легком режиме работы кранов на выносливость не рассчитываются.

3.57 (3.48). Расчет на выносливость сечений, нормальных к продольной оси элементов, должен производиться из условий:

а) для сжатого бетона

               σb,max ≤ Rb ,        (150)

где σb,max — максимальное нормальное напряжение в сжатом бетоне;

Rb — расчетное сопротивление бетона сжатию, принимаемое по табл. 13 при γb2=1,0 и умноженное на коэффициент условий работы γb1,  определяемый согласно п. 3.60;

б) для растянутой арматуры

               σs,max ≤ Rs ,        (151)

где σs,max —  максимальное напряжение в растянутой арматуре, определяемое по формуле

               σs,max=α' σbs + σsp ,        (152)

здесь α' — коэффициент приведения арматуры к бетону, принимаемый по табл. 34;

σbs — напряжение в бетоне на уровне наиболее растянутого ряда арматуры;

σsp — принимается при коэффициенте γsp < 1,0;

Rs — расчетное сопротивление растянутой арматуры, умноженное на коэффициент условий работы γb3, а при наличии сварных соединений — также на коэффициент γs4, определяемое согласно п. 3.61.

Таблица 34

Напряжения σb,max и σbs определяются от действия внешних нагрузок и от усилия предварительного обжатия Р как для упругого тела (см. п. 1.21) по приведенному сечению, принятому согласно п. 3.58.

В зоне, проверяемой по сжатому бетону, при действии многократно повторяющейся нагрузки следует избегать возникновения растягивающих напряжении.

Сжатая арматура на выносливость не рассчитывается.

3.58. При расчете на выносливость приведенное сечение принимается следующим образом:

если в сечении не образуются нормальные трещины, т.е. если выполняется условие (182) при замене в нем значения Rbt,ser на Rbt (при учете γb1), приведенное сечение включает в себя полное сечение бетона, а также площадь сечения всей продольной арматуры, умноженной на коэффициент приведения α′, определяемый по табл. 34;

если в сечении образуются нормальные трещины, приведенное сечение включает в себя площадь сечения только сжатого бетона, а также площадь сечения всей продольной арматуры, умноженную на коэффициент α'.

В этом случае высота сжатой зоны х для изгибаемых элементов определяется из уравнения

,        (153)

где enp — расстояние от нейтральной линии до точки приложения усилия P:

               enp=y' + е0p - x ;        (154)

здесь у' — расстояние от центра тяжести полного приведенного сечения до наиболее сжатой грани;

Ib — момент инерции сжатой зоны бетона относительно нейтральной линии;

Sb, Ssp, Ss, S′sp, S′s — соответственно статические моменты сжатой зоны бетона  и сечений напрягаемой и ненапрягаемой арматуры S и S′ относительно нейтральной линии;

уsp, у'sp, ys, y′s — расстояния от нейтральной линии соответственно до центра тяжести сечений напрягаемой и ненапрягаемой арматуры S и S' (черт. 35).

Черт. 35. Схема расположения усилий в поперечном сечении
с трещиной, рассчитываемом на выносливость

Для изгибаемых элементов, выполняемых без предварительного напряжения, уравнение (153) принимает вид

               Sb - α'Ss + α'S's=0.        (155)

Для внецентренно сжатых или внецентренно растянутых элементов положение нейтральной линии также определяется из уравнения (153), левая часть которого принимается равной Mn / Ntot , гдеMn — момент внешней силы N и усилия обжатия Р относительно нейтральной линии; Ntot=Р ± N (знак «плюс» принимается при сжимающей силе N, знак «минус» — при растягивающей силе N).

Если точка приложения растягивающей силы Ntot (определенная с учетом всех внешних воздействий) находится между центрами тяжести арматуры S и S', в сечении возникают только растягивающие напряжения и в приведенном сечении учитывается только площадь сечения арматуры.

Для элементов прямоугольного, таврового или двутаврового сечений при наличии нормальных трещин уравнение (153) приобретает вид

       ;        (156)

для изгибаемых элементов

es,tot= + esp ;

для внецентренно нагруженных элементов:

es,tot= ;

;    ;    .

Полученное из уравнения (156) значение ξ=x/h0 должно удовлетворять условиям ξ ≥ δ и ξ ≤ (h - hf) / h0.

При отсутствии в сжатой зоне свесов в уравнении (156) принимается δf=2a′ / h0.

Для предварительно напряженных конструкций, у которых не образуются нормальные трещины, характеристики приведенного сечения допускается определять при коэффициенте приведения α=Es / Eb .

3.59 (3.49). Расчет на выносливость сечений, наклонных к продольной оси элемента, должен производиться из условия, что равнодействующая главных растягивающих напряжений, действующих на уровне центра тяжести приведенного сечения, должна быть полностью воспринята поперечной арматурой при напряжениях в ней, равных сопротивлениям Rs, т.е. должно выполняться условие

,        (157)

где σmt - главное растягивающее напряжение на уровне центра тяжести приведенного сечения, вычисляемое согласно п. 4.9;

σy, τху - соответственно сжимающее напряжение в направлении, перпендикулярном продольной оси, и касательное напряжение, определяемые на том же уровне, что и напряжение σmt, согласно пп. 4.10-4.12;

Rs - расчетное сопротивление хомутов и отгибов с учетом коэффициентов условий работы γs3 и γs4 (см. п. 3.61);

θ - угол наклона отгибов к продольной оси элемента на уровне центра тяжести сечения в рассматриваемом сечении;

sinc - расстояние между плоскостями отгибов, измеренное по нормали к ним; при одной плоскости отгибов за sinc принимается расстояние между этой плоскостью и гранью опоры; при двух и более плоскостях отгибов значение sinc определяется согласно черт. 36.

Черт. 36. Учет отогнутых стержней при расчете наклонных сечений
на выносливость

1-1, 2-2 - плоскости отгибов; для 1-1 sinc=(sinc1 + sinc2)/2; для 2-2 sinc=sinc2; l1 и l2 - длины участков элемента при учете соответственно плоскостей отгибов 1-1 и 2-2

Отгибы учитываются в расчете, если расстояние от грани опоры до начала первого отгиба (s1), а также расстояние между концом предыдущего и началом следующего отгиба (s2) не превышают 0,2h (см. черт. 36).

При вычислении σmt, σу и τxy приведенное сечение определяется согласно п. 3.58.

Расчет производится для каждого участка с постоянной интенсивностью поперечного армирования. При наличии отгибов учитывается среднее значение σmt на участке рассматриваемого отгиба (см. черт. 36).

Для элементов, в которых поперечная арматура не предусматривается (см. п. 5.41), должны быть выполнены требования п. 4.9 при замене в условиях (183) и (184) расчетных сопротивлений бетона Rb,ser и Rbt,ser соответственно расчетными сопротивлениями Rb и Rbt, умноженными на коэффициент условий работы γb1 согласно табл. 35.

Таблица 35 (16)

Расчет на выносливость наклонных сечений коротких консолей, поддерживающих подкрановые балки и т.п. конструкции, производится согласно п. 3.99 «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов, выполняемых без предварительного напряжения арматуры», принимая расчетные сопротивления бетона Rb и Rbt с учетом коэффициента γb1.

3.60. Коэффициенты условий работы бетона γb1, применяемые при действии многократно повторяющейся нагрузки, определяются в зависимости от коэффициента асимметрии цикла ρb:

                ,        (158)

где σb,min, σb,max - соответственно наименьшее и наибольшее напряжение в бетоне в пределах цикла изменения нагрузки, определяемые согласно пп. 3.57 и 3.58; при этом напряжения принимаются со своими знаками: при проверке условия (150) за положительные принимаются напряжения сжатия, а при проверке условий (182) и (183) - напряжения растяжения.

При ρb ≥ 0 коэффициент γb1 принимается по табл. 35.

При определении расчетного сопротивления Rbt или Rbt,ser, если напряжение растяжения сменяется напряжением сжатия, за величину σb,min принимаются сжимающие напряжения. В этом случае коэффициент γb1 для тяжелого бетона естественной влажности при 0 > ρb ≥ -5 определяется по формуле

       γb1=0,7 - 0,06 |ρb | .        (159)

При γb1=1,00 расчет на выносливость сжатого бетона можно не производить.

При проверке образования наклонных трещин коэффициенты условий работы γb1, вводимые на расчетные сопротивления Rbt (Rbt,ser) и Rb (Rb,ser), определяются соответственно в зависимости от

        и ,        (160)

где σmc,min , σmc,max , σmt,min , σmt,max — соответственно наименьшие и наибольшие главные сжимающие и главные растягивающие напряжения в бетоне в пределах цикла изменения нагрузки, определяемые согласно п. 4.9 по полному приведенному сечению.

При определении напряжений бетона, входящих в формулы (158) и (160), используются такие же нагрузки, что и при расчете на выносливость.

Для изгибаемых элементов, выполняемых без предварительного напряжения, формулы (158) и (160) приобретают вид:

               ;        (158a)

                .        (160a)

При расчете наклонных сечений коротких консолей также принимается ρb=Qmin / Qmax.

Если число циклов повторения нагрузок значительно превышает 2⋅106 (т.е. порядка 10k, где k ≥ 7), коэффициент условий работы γb1 следует уменьшить на 0,03 (k - 6).

3.61 (2.28). Коэффициенты условий работы арматуры γs3, принимаемые при расчете на выносливость, определяются по табл. 36.

Таблица 36 (25)

П р и м е ч а н и е. При значениях ρs, для которых в табл. 36 не даны значения коэффициента γs3, применение соответствующей арматуры не допускается.

При наличии сварных соединений учитывается дополнительный коэффициент условий работы γs4, определяемый по табл. 37.

Таблица 37 (26)

П р и м е ч а н и я: 1. Группы сварных соединений, приведенные в настоящей таблице, включают следующие типы соединений, допускаемые для конструкций, рассчитываемых на выносливость, и приведенные в обязательных приложениях 3 и 4 СНиП 2.03.01-84:

1-я группа — стыковое - по поз. 6 обязательного приложения 3;

2-я    «       — крестообразное - по поз. 1, стыковые - по поз. 5, 8 и 9, а также по поз. 10-12 и 25 - все соединения при отношении диаметров стержней, равном 1,0 (см. обязательное приложение 3); тавровые - по поз. 5 и 7 обязательного приложения 4;

3-я    «      — крестообразные - по поз. 2 и 4, стыковые - по поз. 13-26 обязательного приложения 3; тавровые - по поз. 1-4, 6, 8, 9 обязательного приложения 4.

2. В таблице даны значения γs4 для арматуры диаметром до 20 мм.

3. Значения коэффициента γs4 должны быть снижены на 5 % при диаметре стержней 22-32 мм и на 10 % при диаметре свыше 32 мм.

4. В конструкциях, рассчитываемых на выносливость, соединения по поз. 3 и 27 обязательного приложения 3, а также по поз. 10-14 обязательного приложения 4 применять не допускается.

При расчете на выносливость нормальных сечений коэффициент асимметрии цикла ρs определяется по формуле

                ,        (161)

где σs,min, σs,max - соответственно наименьшее и наибольшее напряжения в растянутой арматуре в пределах цикла изменения нагрузки, определяемые согласно пп. 3.57 и 3.58; при этом растягивающие напряжения принимаются со знаком «плюс», а сжимающие напряжения — со знаком «минус».

При расчете изгибаемых элементов из тяжелого бетона с ненапрягаемой арматурой значение ρs для продольной арматуры принимается:

при 0 ≤ ≤ 0,2                ρs=0,3 ;

при 0,2 < ≤ 0,75        ρs=0,15 + 0,8 ;

при > 0,75                    ρs=  ,

где Mmin, Mmax - соответственно наименьший и наибольший изгибающие моменты в расчетном сечении элемента в пределах цикла изменения нагрузки.

При расчете на выносливость наклонных сечений значение ρs  определяется по формуле

               ρs= ,        (162)

где σmt,min , σmt,max - соответственно наименьшие и наибольшие главные растягивающие напряжения в бетоне в пределах цикла изменения нагрузки, определяемые согласно п. 4.9 с учетом п. 3.58.

Для изгибаемых элементов с ненапрягаемой арматурой формула (162) приобретает вид

               ρs=.        (162a)

При вычислении напряжений и усилий, входящих во все формулы для ρs, используются те же нагрузки, что и при расчете на выносливость.

При γs3 и γs4=1,00 расчет на выносливость растянутой арматуры можно не производить.

Примеры расчета

Пример 27. Дано: предварительно напряженная подкрановая балка с поперечным сечением по черт. 37, а; бетон тяжелый класса В30; геометрические характеристики приведенного поперечного сечения (определенные при коэффициенте приведения α=Еs / Еb): площадь Ared=339 100 мм2; расстояние от центра тяжести сечения до нижней грани y0=728 мм, момент инерции Ired=85 850 • 106 мм4, продольная арматура S и S' — предварительно напряженная класса A-IV, площадью соответственно Asp=4021 мм2 и A'sp=942 мм2; поперечная арматура в виде сварных хомутов класса A-III, диаметром 12 мм, шагом 100 мм, по два в сечении; усилие предварительного обжатия с учетом всех потерь напряжений Р=1536 кН, его эксцентриситет относительно центра тяжести сечения e0p=357 мм; предварительное напряжение с учетом всех потерь в арматуре S σsp=290 МПа; нагрузка: сосредоточенная от крана F=290 кН, равномерно распределенная от собственного веса балки и подкранового пути g=11 кН/м; случаи невыгоднейшего расположения кранов приведены на черт. 37,б,в; краны — среднего режима работы; расчетный пролет балки 11,7 м.

Требуется рассчитать подкрановую балку на выносливость по нормальным и наклонным сечениям.

Черт. 37. К примеру расчета 27

а - поперечное сечение балки; б, в - схемы невыгоднейшего
расположения нагрузки; 1 - центр тяжести приведенного сечения;
2 - точка приложения усилия обжатия Р

Р а с ч е т. Рассчитаем нормальные сечения. Определим наибольший изгибающий момент в сечении I-I при невыгоднейшем расположении крана (см. черт. 37, б) :

Мmax=290=1229 кН⋅м.

Наименьший изгибающий момент в сечении I-I (при отсутствии крана) равен:

Mmin==180 кН⋅м.

Проверяем возможность образования трещин в растянутой зоне согласно п. 4.8. Для этого определяем напряжения бетона по нижней грани σb,max и σb,min - учитывая полное приведенное сечение (при α=Еs/Еb).

От действия усилия P сжимающее напряжение по нижней грани равно:

=9,2 МПа.

Тогда

=1,22 МПа ;

=-7,67 МПа < 0 ,

т.e. при действии момента Mmin сечение полностью сжато.

Поскольку σb,max=1,22 МПа > Rbt=1,2 МПа, т.e. даже без учета коэффициента γb1 условие (182) не выполняется, трещины в растянутой зоне образуются.

Согласно п. 3.58, приведенное сечение определяется без учета растянутого бетона.

Относительную высоту сжатой зоны ξ определяем из уравнения (156). Для этого находим величины φf , esp , es,tot , μα′ и δf.

Из табл. 34 находим α′=15; h0=n - a=1400 - 60=1340 мм;

=0,47 ;

esp=y0 - e0p - a=728 - 357 - 60=311 мм ;

=1110 мм ;

μα′==0,322 ;

=0,15 .

Представляя уравнение (156) в виде

f(ξ)=ξ3 - aξ2 + bξ + c=0 ,

определяем коэффициенты a, b и с:

=0,515 ;

       =1,33 ;

Таким образом, f(ξ)=ξ3 - 0,515ξ2 + 1,33ξ - 1,585=0.

Решаем уравнение методом Ньютона. Первая производная выражения f(ξ) имеет вид

f(ξ)=3ξ2 - 2aξ + b=3ξ2 - 1,03ξ + 1,33 .

Принимая ξ0=1, получим в первом приближении

Во втором приближении, принимая ξ0=ξ1=0,93, получим

Поскольку ξ2 мало отличается от ξ1, окончательно принимаем ξ=ξ2 =0,93, т.е. х=ξh0=0,93 ⋅ 1340=1246 мм.

Определяем характеристики приведенного сечения без учета растянутого бетона:

площадь

Ared=510⋅200 + 140(1246-200) + 15⋅942 + 15⋅4021=322 880 мм2;

статический момент относительно растянутой арматуры

Sred=510 ⋅ 200(1340 - 100) + 140 ⋅ 1046+

+ 15⋅942(1340 - 40)=235,2 ⋅ 106 мм3 ;

расстояние от центра тяжести сечения до растянутой арматуры

728 мм ;

момент инерции

+ 140⋅1046⋅1112 + 15⋅942⋅5722 + 15⋅4021⋅7282=78820 ⋅ 106 мм4 ;

расстояние от усилия Р до центра тяжести сечения

e0p=ysp - esp=728 - 311=417 мм .

Проверяем выносливость сжатого бетона из условия (150). Для этого определяем наибольшие и наименьшие напряжения σb,max и σb,min в верхнем краевом волокне бетона, т.е. на расстоянии у′=1340 - 728=612 мм от центра тяжести сечения:

=9,3 МПа .

Вследствие того, что при минимальной внешней нагрузке напряжения в бетоне по нижней грани сжимающие, напряжения в верхнем волокне бетона при этой нагрузке будем определять по полному приведенному сечению, т.е. при Ared=339 100 мм2; Ired=85 850 • 106 мм4; e0p=357 мм; у′=1400 - 728=672 мм:

=1,65 МПа > 0,

т.е. растягивающие напряжения в верхней зоне не появляются.

Коэффициент асимметрии цикла найдем по формуле (158) :

ρb=σb,min / σb,max=1,65 / 9,3=0,177.

По табл. 35 при ρb=0,177 найдем γb1=0,79;

Rb =0,79 ⋅ 17=13,4 МПа > σb,max=9,3 МПа,

т.е. выносливость сжатого бетона обеспечена.

Проверяем выносливость растянутой арматуры из условия (151). Определяем наибольшие и наименьшие напряжения σs,max и σs,min на уровне растянутой арматуры по формуле (152):

=300 МПа ;

=179 МПа .

По формуле (161) находим коэффициент асимметрии цикла напряжений в арматуре:

=0,60 .

По табл. 36 при ρs=0,60 и классе арматуры A-IV находим γs3=0,61:

Rs=0,61 • 510=311 МПа > σs,max=300 МПа,

т.е. выносливость растянутой арматуры обеспечена.

Рассчитаем на выносливость наклонные сечения.

Определяем изгибающий момент и поперечную силу в сечении II-II:

а) при невыгоднейшем расположении крана

=400 кН⋅м ;

=416 кН ;

б) при отсутствии крана

Qmin=11=54 кН.

Аналогично вышеуказанному проверяем возможность образования нормальных трещин в этом сечении:

МПа < 0 ,

т.е. при действии Мmax все сечение сжато и трещины отсутствуют, поэтому расчет ведем по полному приведенному сечению.

Выносливость наклонных сечений проверяем на уровне центра тяжести приведенного сечения. Определяем статический момент верхней части Sred сечения относительно этого уровня, принимая

=6,55 ;

Sred=510 ⋅ 200+ 140(672 - 200) 0,5 + 6,55 ⋅ 942(672 - 40)=

=77,84 ⋅ 106 мм3 .

Наибольшие и наименьшие касательные напряжения определяем по формуле (189):

2,69 МПа ;

0,35 МПа .

Нормальные напряжения на уровне центра тяжести сечения не зависят от внешней нагрузки и равны:

=4,52 МПа .

Поскольку сечение II-II расположено от опоры и от первого груза на расстоянии 0,95 м ≈ 0,7h, принимаем напряжение σу=σy,loc=0.

Определяем по формуле (185) наибольшие и наименьшие главные растягивающие напряжения:

=

-2,26 + 3,52=1,26 МПа ;

=

=-2,26 + =0,027 МПа .

Коэффициент асимметрии цикла для поперечной арматуры равен:

=0,0214 .

По табл. 36 при ρs=0,0214 и классе арматуры А-III находим γb3=0,405. Поскольку поперечные стержни приварены к продольным точечной сваркой (поз. 1 обязательного прил. 3 СНиП 2.03.01-84), по табл. 37 при ρs=0,0214, классе арматуры А-III и 2-й группе сварных соединений находим γs4=0,605. Отсюда Rs=0,405 • 0,605 • 365=89,4 МПа.

Проверяем условие (157), принимая Asw=226 мм2 (2∅12) и Аs,inc=0:RsAsw=89,4 • 226/(140 • 100)=1,44 МПа > σmt,max=1,26 МПа, т.е. выносливость наклонных сечений обеспечена.

> Категории: Системы стандартов строительство дачных домов Единые нормы и расценки Кодексы строительные нормы и правила деревянный дом сметные нормы снип

Поделитесь этой записью или добавьте в закладки