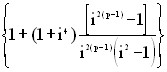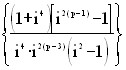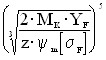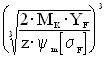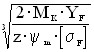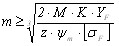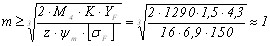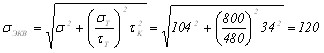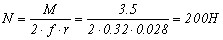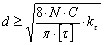Содержание
I. Введение 1. ЭМП (классификация, назначение и применение). [3] Электромеханическим приводом (ЭМП) называется устройство, состоящее из двух основных частей: электродвигателя, осуществляющего преобразование электрической энергии в механическую, и редуктора, связывающего электродвигатель с рабочим органом. Рабочий орган создаёт нагрузку на выходном или рабочем валу редуктора. Блок-схема ЭМП показана на рис. 1, где 1 - электродвигатель; 2 - редуктор; 3 - рабочий орган. ЭМП в литературе часто называют исполнительным механизмом, так как именно он приводит в действие рабочий орган. В зависимости от характера работы ЭМП можно разбить на две категории: нерегулируемые ЭМП и регулируемый, или следящий, ЭМП. Регулируемым, или следящим, ЭМП является более сложным устройством; его применяют в автоматических системах управления или регулирования. Для следящего электромеханического привода характерны повторно-кратковременный режим работы, высокое быстродействие, большая частота пусков и реверсов. Следящий электромеханический привод применяют в измерительных приборах, основанных на автоматическом компенсационном методе измерения, в системах автоматического регулирования промышленными процессами, в автопилотах, в радиолокационных установках для поиска и слежения за перемещающимися объектами, в автоматических прицелах, в следящих системах дистанционных передач и т. д. В регулируемых приводах помимо элементов управления, блокировки и сигнализации имеются датчики обратной связи по углу и скорости, элементы дистанционных передач, отсчётные механизмы высокой точности. Регулируемый (следящий) привод работает в условиях постоянного реверса, поэтому здесь на первый план выдвигаются инерционные (динамические) нагрузки. В следствии этого, к приводу предъявляются требования малой инерционности, уменьшения момента трогания (начального момента трения), снижения мёртвого хода, увеличения кинематической точности редуктора, виброустойчивости при разных режимах работы. Во всех случаях проектирования ЭМП, а при проектировании привода летательных аппаратов в особенности, необходимо стремиться к снижению габаритов и массы механизмов. Проектирование и конструирование ЭМП существенно зависит от того, в состав какого устройства входит привод, является ли он регулируемым или нерегулируемым. Однако основные вопросы, относящиеся к проектированию ЭМП, являются общими для разных видов привода. При проектировании ЭМП необходимо правильно выбрать тип двигателя, найти передаточное число редуктора и спроектировать редуктор.
2. Обоснование выбора материалов и отдельных конструктивных решений I. Обоснование выбора материалов [2]. Материал выбирают с учётом назначения передачи, характера действующей нагрузки, условий эксплуатации (окружной скорости, состояния среды), массы, габаритов и стоимости. Желательно количество материалов, используемых в разрабатываемом приводе, резко ограничить. При небольших окружных скоростях V (до 3 м/с) для изготовления мелкомодульных цилиндрических и конических передач применяют конструктивные стали 35, 40, 45, 50 (по ГОСТ 1050-74) как в сыром, так и в термоулучшенном виде (HRC 28..32). При повышенных окружных скоростях применяют легированные стали 40Х, 45Х, 2Х13, 40ХН и другие (по ГОСТ 4543-71). Зубчатые колёса подвергают закалке до НВ 300. Колёса с повышенной антикоррозионной устойчивостью изготавливают из стали ЭИ474 (ГОСТ 4543-71), а с повышенной износостойкостью - из стали 38ХМЮА (ГОСТ 4543-71) при закалке до НВ 260, азотировании НВ 500. Для нагруженных трибок применяют также стали У8А, У10А по ГОСТ 1435-74 с закалкой до HRC 40..64, стали 2Х13, 4Х13 в термоулучшенном виде (HRC 28..32). Для малонагруженных зубчатых передач применяют бронзы БрКМц 3-1Т, БрАМц 9-2Т, БрОЦ 4-3Т, БрОФ 6,5-0,15Т, латуни ЛС59-1Т (по ГОСТ 15527-71), а также алюминиевые сплавы Д16Т, Д1АТ и ВТ95Т1 (по ГОСТ 4784-74) при требованиях малой массы, момента инерции, частоты вращения менее 1000 об/мин. Для прирабатывающихся зубчатых передач (твёрдость рабочих поверхностей колёс НВ=350 (1 НВ ≈ 10 HRC)) рекомендуется для выравнивания срока службы назначать для зубчатых колёс разные материалы, причём твёрдость шестерни должна быть на 20..30 единиц больше твёрдости колеса НВ1=НВ2 + 20..30. Для цилиндрических прямозубых шестерни и колеса рекомендуются следующие пары материалов соответственно: при V до 15 м/с сталь 15Х - сталь 50, 55; сталь 55 - сталь 45, 50; сталь 45 - бронза БрАЖ9-4; при V до 6 м/с сталь 45 - сталь 35; сталь15 - алюминиевый сплав Д16Т. Для неприрабатывающихся зубчатых передач с твёрдыми рабочими поверхностями зубьев обоих зубчатых колёс (твёрдость HRC > 45) обеспечивать разность твёрдостей зубьев шестерни и колеса не требуются. Стали углеродистые качественные (по ГОСТ 1050-74) имеют более жёсткие допуски на химический состав и механические характеристики, чем стали углеродистые общего назначения. Это позволяет получить тонкую градацию технологических свойств стали и гарантировать заданное качество изготавливаемых из неё деталей. Низкоуглеродистые стали этой группы (05кп, 08кп, 08пс, 08, 10кп, 10пс, 10, 15кп, 15пс, 15, 20кп, 20пс, 20, 25) обладают высокой пластичностью и свариваемостью. Из листовой стали этих марок можно изготавливать штамповые и свариваемые кожухи, детали глубокой втяжки, корпуса, детали, получаемые развальцовкой и гибкой, рычаги кронштейны и тому подобное. При цементации и цианировани эти стали приобретают высокую твёрдость поверхности, что хорошо сохраняет детали из них при работе на истирание (различные пальцы шарнирных соединений, кулачки, зубчатые звёздочки, детали неответственных направляющих и каретки). Стали 40 и 45 обычно применяют как улучшаемые стали, обеспечивающие высокую твёрдость поверхности детали и высокие механические характеристики. Из этих сталей для приборов можно изготовлять зубчатые передачи. Выберем для колёс материал сталь 45, валов и муфты материал сталь 40Х, а для платы сталь 20, которые имеют характеристики:
где σВ — временное сопротивление (предел прочности при растяжении); σТ — предел текучести при растяжении; σ-1 — предел выносливости материала при симметричном цикле нагружения τ-1 — предел выносливости при кручении. II. Обоснование распределения передаточного отношения i0, влияние приведённого момента инерции JР ПР редуктора и пути его уменьшения [1]. Одним из главных вопросов кинематических расчётов является распределение общего передаточного отношения i0 по ступеням передачи, поскольку от него зависят основные характеристики редуктора и привода в целом. В литературе можно встретить рекомендации по решению этой задачи при условии минимизации массы, габаритов, инерционных и точностных характеристик передачи привода. Следует однако особо подчеркнуть, что эти рекомендации и выводы получены при ряде упрощающих предположений и не учитывают особенностей реального конструирования, а также значительное число во многом противоречивых требований, которые предъявляются к приводу. Опыт реального проектирования показывает, что упомянутые рекомендации по распределению i0 в большинстве случаев не приносят желаемого результата. Задачу распределения i0 по ступеням передачи нельзя рассматривать как отдельную, независимую и чисто теоретическую, отвлечённую от практической стороны задачу, а как неотъемлемую часть синтеза привода в целом. И, таким образом, решение её должно носить комплексный характер. Для иллюстрации сказанного остановимся более подробно на частной задаче распределения i0 с целью повышения быстродействия привода, что достигается минимизацией его привидённого момента инерции JР ПР. Для наиболее употребительных многоступенчатых передач цилиндрическими колёсами JПР записывают в таком виде: JПР = JДВ + JР ПР + JН ПР = JДВ +( J1 + J2 / i122 +...+ JК / i1К2 +...+ Jn / i1n2 )+ JН / i1n2, где JДВ — момент инерции ротора двигателя; JР ПР — привидённый момент инерции передач (редуктора); JН ПР — привидённый момент инерции нагрузки; J1, J2, . . . , JК, . . . , Jn — момент инерции вращающихся элементов передачи (зубчатых передач, колёс, муфт и т. п.), связанных соответственно с валами 1, 2, , . . . , к, . . . , n; i12, i13, . . . , i1К, . . . , i1n — передаточные отношения между первым и последующими валами (i1n = i0). Согласно известным исследованиям относительный минимум JПР достигается при оптимальном числе ступеней редуктора nopt = 3lgi0 и сугубо неравномерном распределении i0 по ступеням — постепенном увеличении передаточных отношений от входа к выходу редуктора. Одним из главных недостатков известного подхода к повышению быстродействия электромеханических прмводов является игнорирование момента инерции ротора двигателя JДВ. Проведём сравнение JР ПР и JДВ, чтобы выяснить долю JР ПР в JПР и решить вопрос, насколько вообще имеет смысл заниматься математической минимизацией JР ПР как части общего момента инерции привода. Примем наиболее простое и часто встречающееся на практике равномерное распределение i0 по ступеням, сохраняя другие допущения при «оптимальном» распределении. То есть будем считать, что передаточные отношения ступеней одинаковы i12 = i23 = . . . = i(n-1)n = i, тогда будут равны между собой не только моменты инерции шестерён JШ во всех ступенях, но и моменты инерции больших колёс JК (разумеется, одинаков будет во всех ступенях и модуль). Тогда JР ПР можно записать в виде JПР = JШ + (JК + JШ)/i2 + (JК + JШ)/i4 + . . . + (JК + JШ)/i2(n-2) + JК/i2(n-1) ≈ ≈ JШ + (JК + JШ)/i2 + (JК + JШ)/i4 + . . . + ( JК + JШ)/i2(n-2) , ⊕ где n — номер вала редуктора, причём считаем, что i2(n-1) « JР ПР. Замечая, что все члены в этой сумме, следующие за JШ, составляют убывающую геометрическую прогрессию, первый член которой a1 = (JК + JШ)/i2, а знаменатель q =1/i2, и учитывая, что JК = JШ⋅ i4, выражение ⊕ преобразуем к виду JПР = JШ + где p=n-1 — число ступеней. Момент инерции всех ступеней, следующих за второй (а точнее, момент инерции всех элементов , следующих за третьим валом, не считая колеса последней ступени) запишется JОСТ = Разделив JОСТ на JР ПР, получим
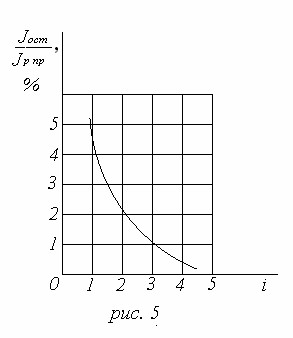
где
Функция ⊗ изображена на рис. 1. Из него следует, что при i ≥ 3 . . 4 значение инерции элементов на первых валах редуктора, а по существу привидённым моментом инерции двух первых ступеней. (Если этот вывод справедлив при одинаковых модулях во всех ступенях, то тем более он будет справедливи при реальных значениях m, ибо m первых ступеней, а следовательно, JШ и JК здесь могут быть только меньше по сравнению с теми же величинами в остальной части редуктора.) Оценивая JР ПР мы видим что он составляет несколько процентов от JДВ, причём основная часть его есть момент инерции колеса первой ступени. Заметим, что при разработке реальной конструкции в некоторых случаях размеры шестерни первой ступени придётся увеличивать, чтобы можно было нормально закрепить её на валу двигателя. Это естественно повлечёт за собой увеличение JШ, а также JК первой ступени ( если сохранить в ней передаточное отношение) и, следовательно JР ПР. При этом однако не следует забывать и возможности уменьшения JР ПР, особенно за счёт снижения момента инерции большого колеса первой ступени, доля которого в JР ПР доминирующая. Как известно, значительное уменьшение JК наиболее просто можно получить утонением стенки колеса с помощью боковых проточек, а также использованием в колесе облегчающих отверстий. Оценочные расчёты показывают, что при всём при этом указанное выше соотношение между JР ПР и JДВ существенно не измениться, и можно считать, что в реальных конструкциях при грамотном подходе к проектированию JР ПР не превысит 5% от JДВ. Таким образом для быстродействующих приводов вполне приемлемо равномерное распределение общего передаточного отношения по ступеням, назначенное из соображений простоты конструкции, унификации узлов и прочих требований, предъявляемых к устройству. Для грамотно разработанной конструкции таких приводов можно принять JР ПР = 0, а их динамику расчитать принимая JР ПР = JДВ + JН/ i02. В заключении отметим особенности выбора числа зубьев z колёс передачи, обеспечивающих реализацию передаточных отношений ступеней и редуктора в целом. По этому вопросу полезно сделать два замечания. Первое: в управляемых и в большинстве неуправляемых приводов точная реализация i отдельных ступеней и общего i0 вовсе необязательна. В управляемых приводах скорость входного вала определяется не столько i0 (или моментом нагрузки), сколько системой управления привода. Эта система всегда скомпенсирует незначительные отклонения действительных значений i0 от расчётных изменением скорости вращения двигателя. В большинстве неуправляемых приводов допустимы определённые отклонения от заданной скорости элемента нагрузки, поэтому и здесь возможны некоторые отклонения i0 от расчётных значений. Второе замечание касается чисел зубьев шестерен. Необходимо помнить, что zШ может оказать существенное влияние на такие характеристики привода как момент инерции, масса и габариты колеса и, следовательно, момент инерции, масса и габариты привода. Рассчитаем зависимость J(z) (она справедлива как для JК, так и для JШ ,с соответствующими параметрами) : J = π⋅b(d/2)4⋅ρ/2 = π⋅ψm Здесь в постоянную A включены все величины, кроме z, причём принято YF = const. Показателем массы передачи (привода) можно считать массу одного колеса Vρ = πd2ρb/4=π⋅ψm⋅ρ⋅z2 где V — объём колеса; B — постоянная, подобная A. И, наконец, в качестве показателя габаритов примем диаметр колеса d = mz = Из формул (1),(2) и (3) видно, что момент инерции, масса и габариты привода могут быть существенно снижены путём уменьшения z. II. Расчёт параметров конструкции [3] В приборостроении нашли широкое применение как редукторы — передачи, понижающие угловую скорость, так и мультипликаторы — передачи, увеличивающие угловую скорость от входа к выходу. Редукторы применяют в основном в различного рода приводах, а мультипликаторы — в отсчётных передачах измерительных приборов. Требования к зубчатым передачам определяются в первую очередь назначением приборного устройства, для которого они проектируются. Редукторы нерегулируемого силового привода длительного действия должны удовлетворять требованиям равнопрочности, высокого к. п. д., иметь большой ресурс работы, в ряде случаев должны обеспечивать высокую плавность работы. Редукторы следящих приводов, а также редукторы быстродействующих старт-стопных механизмов периферийных устройств ЭВМ должны удовлетворять требованиям обратимости хода, минимального мёртвого хода, уменьшения инерционности. Редукторы преобразователей, требующих повышенной точности согласования движения входного и выходного звеньев, а также прецизионные отсчётные передачи должны удовлетворять требованиям минимального трения, минимального мёртвого хода и повышенной кинематической точности передачи. Во всех случаях проектирования, а особенно при проектировании механизмов, предназначенных для летательных аппаратов, необходимо обеспечить высокую надёжность передачи и целесообразное уменьшение её массы и габаритов. При проектировании любого вида зубчатой передачи перед конструктором-расчётчиком возникает целый ряд вопросов, которые он должен решить в определённой последовательности. К числу основных вопросов относятся следующие: определение общего передаточного отношения; выбор типа передачи и вида зацепления; определение количества ступеней в передаче и распределения передаточного отношения по ступеням; определение числа зубьев колёс, расчёт на прочность и определение модуля зацепления; определение геометрических параметров колёс; расчёт сил и моментов, определение к. п. д. Передачи, определение мощности на входе редуктора; расчёт передач на точность, выбор стенки точности колёс, вида сопряжения, определение мёртвого хода и кинематической погрешности передачи; расчёт валов и подбор подшипников. Технические характеристики проектируемого ЭМП
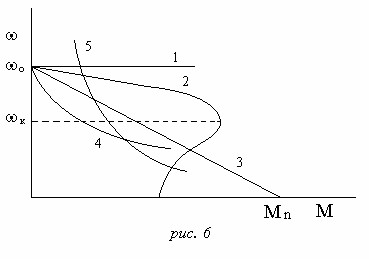
где: МН max — максимальный момент нагрузки на выходном валу привода; ωн max — максимальная угловая скорость выходного вала; ω′Н MAX — максимальное угловое ускорение выходного вала; JН — момент инерции элемента нагрузки; Uп — напряжение питания сети. 1. Подбор двигателя. Общие рекомендации по выбору двигателя. При подборе электродвигателя руководствуются следующими показателями: родом тока, номинальным напряжением питания, мощностью и частотой вращения, номинальным и пусковым моментом, жёсткостью (мягкостью) характеристики, регулировочными свойствами, стойкостью к внешним воздействиям. При этом стремятся выбрать наиболее простой по конструкции и управлению электродвигатель, надёжный и имеющий минимальную стоимость и массу, с высоким КПД. Также он должен обеспечивать выполнение приводом его функций. Механической характеристикой электродвигателя называют зависимость частоты вращения вала электродвигателя от момента нагрузки на валу. В дальнейшем механическую характеристику будем называть просто характеристикой. На рис.2 приведены характеристики наиболее часто применяемых электродвигателей.
Характеристика вида 1 назы-вается линейной абсолютно жёсткой. Она свойственна синхронным электродвигателям, двигателям постоянного тока с регуляторами скорости и некоторым типам электродвигателей постоянного тока с бесконтактными коммутаци-онными устройствами. Характеристика вида 2 сугубо нелинейная, принадлежит асинхронным двигателям. Характеристика может считаться линейной (в первом приближении) до 2/3 ωК. Характеристика вида 3 Жёсткая линейная, принадлежит двигателям постоянного тока независимого возбуждения (якорное управление) и с возбуждением от постоянных магнитов. Характеристика вида 4 мягкая, она свойственна электродвигателям со смешанным возбуждением. Характеристика вида 5 мягкая, принадлежит электродвигателям постоянного тока последовательного возбуждения. Наиболее просты и надёжны асинхронные электродвигатели с короткозамкнутым ротором. Их масса в 1,5..2,0 раза меньше двигателей постоянного тока той же мощности. Питание осуществляется непосредственно от сети переменного тока. Электродвигатели используются в системах автоматизированного приборного привода при небольшой частоте включения, когда не требуется плавная регулировка частоты вращения. В приводах с глубоким регулированием частоты вращения применяют двух фазные управляемые асинхронные двигатели различного вида исполнения. В приводах, требующих плавного и глубокого регулирования частоты вращения, высокого качество переходных процессов, применяются электродвигатели постоянного тока с независимым возбуждением. Они обладают наилучшими регулировочными и пусковыми характеристиками при высоких энергетических показателях. В особо тяжёлых условиях работы применяют бесконтактные электродвигатели постоянного тока. Синхронные электродвигатели и двигатели постоянного тока с регуляторами скорости вращения используют в приводах лентопротяжных устройств, программных механизмах, электромеханических реле времени, часовых механизмов и других устройствах, где требуется соблюдать точные временные масштабы. Выбор электродвигателя следящей системы. Задача выбора электродвигателя следящего привода достаточно достаточно точно может быть решена при наличии статических характеристик конкретного привода. Чаще всего такие характеристики отсутствуют. В этом случае потребную мощность определяют исходя из её максимального значения. По найденному значению мощности по каталогу определяют тип двигателя. Для приводов следящих систем используют двигатели:
Согласно техническим характеристикам рассматриваемого привода (Uп = 12В, сеть постоянного тока, срок службы двигателя 2500 часов) существенно сужается круг рассматриваемых двигателей, таким образом нашим требованиям удовлетворяют следующие двигатели со своими характеристиками:
Проверим соответствие номинальных мощностей этих двигателей с расчётной мощностью нагрузки. Необходимая расчётная мощность определяется по формуле: PP ≈ где i0 — общее передаточное отношение передачи; η0 — предполагаемый к. п. д.; JПР — приведённый момент инерции двигателя: JПР = JР + JПР/ i02 ; i0 = ωДВном / ωнmax ; ωДВном = nНОМ⋅2π/60 ; η0 = η1n , где η1 — к. п. д. одной ступени; n — число ступеней; Двигатель ДПР-32-Н1-07: JР = 0,002⋅10-4 кг/м 2 ; ωДВном = nНОМ⋅2π/60 = i0 = ωДВном / ωнmax = Принимаем передаточное отношение для всех колёс одинаковое, то есть
i1= i2 = i3 = . . . = in ⇒ i1n = i0, тогда n = lg (i0)/lg(i1) принимаем i1 = 3,5 . . 5 . Получаем ориентировочное число ступеней n=5 (так как n = lg (i0)/lg(i1) ≈ 4,4 . . 5,2) Принимаем η1 = 0,95, тогда η0 = η1n = 0,955 ≈ 0,77 Вычисляем JПР = JР + JПР/ i02 = 0,002⋅10-4 + 0,5/8732 ≈ 873⋅10 -9 кг⋅м2 Вычисляем расчётную мощность : PP = PНОМ= Двигатель ДПР-42-Н1-08: JР = 0,0057⋅10-4 кг/м 2 ; ωДВном = nНОМ⋅2π/60 = i0 = ωДВном / ωнmax = Вычисляем JПР = JР + JПР/ i02 = 0,0057⋅10-4 + 0,5/8732 ≈ 1,23⋅10 -6 кг⋅м2 Вычисляем расчётную мощность : PP = PНОМ = Двигатель ДПР-52-Н1-08: JР = 0,017⋅10-4 кг/м 2 ; ωДВном = nНОМ⋅2π/60 = i0 = ωДВном / ωнmax = Вычисляем JПР = JР + JПР/ i02 = 0,017⋅10-4 + 0,5/8732 ≈ 2,36⋅10 -6 кг⋅м2 Вычисляем расчётную мощность : PP = PНОМ = Сравним характеристики двигателей:
Сравнивая эти двигатели видим, что в отношении габаритов они практически равноценны. Редукторы будут иметь одинаковое число ступеней. Остановим свой выбор на ДПР-32-Ф1-08, так как нам не нужен большой запас по мощности. Выпишем характеристики ДПР-32-Ф1-08 :
2. Кинематический расчёт Передача цилиндрическими прямозубыми колёсами внешнего зацепления передаёт движение между параллельными валами и является самым распространённым видом передачи, так как обладает целым рядом достоинств, к числу которых надо отнести технологичность конструкции, наибольшую достижимую точность обработки колёс и монтажа их, высокий к. п. д., небольшую стоимость В первую очередь проектант должен остановить свой выбор на этой передаче и отдавать предпочтение другим передачам в случае невозможности удовлетворить требованиям технического задания с помощью передачи цилиндрическими прямозубыми колёсами с внешним зацеплением. Передаточное отношение i = 1 . . 8, причём для эвольвентного зацепления наиболее часто применяются значения 1 . . 6, а для часового и цевочного 6 . . 8. Передача коническими прямозубыми колёсами служит для передачи движения между валами , оси которых пересекаются. Межосевой угол δ выбирается в пределах 10..170°. Чаще всего δ=90°. По сравнению с цилиндрическими передачами обладают меньшей плавностью в работе, меньшей точностью, более низким к. п. д., нетехнологичны в изготовлении, сложны в монтаже. Передаточное отношение i = 1 . . 5. При скоростях V ≥ 2 . . 3 м/с требуют шлифования зубьев. Для правильного монтажа конических колёс необходимо предусмотреть возможность регулирования положения колёс, так как они особенно чувствительны к ошибкам в зацеплении, Недостатком конических колёс является также наличие осевых усилий и необходимость консольного крепления одного из колёс. Желательно избегать применения конических колёс в точных отсчётных передачах. Червячная передача передаёт движение перекрещивающимся валам. Червячная передача отличается компактностью при больших передаточных отношениях и бесшумностью. Однако червячные передачи обычно обладают низким к. п. д., а также возможностью заклинивания при реверсе, если угол подъёма винтовой линии мал. Это ограничивает, а зачастую и исключает возможность их применения в реверсивных передачах следящего привода. Изготовление точных отсчётных червячных передач очень трудоёмко. Передаточное отношение червячной передачи лежит в пределах 7 . . 500. Наиболее употребительным считается диапазон i = 12 . . 150. В отдельных случаях диапазон i может быть расширен от 5 до 1500. Червячная передача требует повышенной точности сборки и нуждается в обильной смазке. Значительные осевые усилия требуют применение радиально-упорных подшипников. Выберем для редуктора цилиндрическую передачу, исходя из требований соосности входа и выхода. Выберем минимальное число зубьев из ряда возможных z = 16 , так как это обеспечивает минимальные массу и габариты привода, и является минимальным из тех, которые могут обеспечить требуемое пердаточное отношение при расчитанном количестве ступеней редуктора. Определим общее передаточное отношение и число ступеней: i0 = ωДВном / ωнmax = Принимаем передаточное отношение для всех колёс одинаковое, то есть i1= i2 = i3 = . . . = in ⇒ i1n = i0. Оптимальное число ступеней редуктора при условии минимума габаритов проектируемого редуктора вычислим по формуле: nопт = 1,85 lg i0 ,принимая i1 = 3,5 . . 5. Получаем ориентировочное число ступеней n = 4 (так как n = lg (i0)/lg(i1) ≈ 3,8 . . 4,1) (кинематическая схема ЭМП прилагается) 2.1. Расчёт моментов Полный момент нагрузки на выходном валу Мвых складывается из статического момента нагрузки МНmax и динамического МДвых:
Запишем формулу для поиска моментов на валах редуктора
где
Зацепление 4: Зацепление 3: Зацепление 2: Зацепление 1: Вывод: Следовательно ДПР-62-Н1-08.
а) пределение модулей зубчатых колёс В связи с тем, что входной и выходной валы редуктора являются соосными, для точной сборки и безупречной работы механизма модуль всех ступеней редуктора выберем одинаковым, рассчитанным для зацепления 4:
где K — коэффициент запаса; M — расчётный момент;
у нас : K = 1,5;
σF = 150 МПа . Итак:
Округляем полученные значения модулей до ближайшего больших из стандартного ряда модулей:
Таким образом имеем: модуль для всех ступеней редуктора выбираем равным б) определение основных размеров всех ступеней редуктора Заметим, что зацепления 1 - 4 являются идентичными, поэтому их размеры будут одинаковыми. Диаметр делительной окружности:
Ширина колёс:
2.3. Расчет валов а) определение диаметров валов Расчётное значение диаметров валов с учётом только нагрузки кручения рассчитывается по формуле:
где диаметр выходного вала
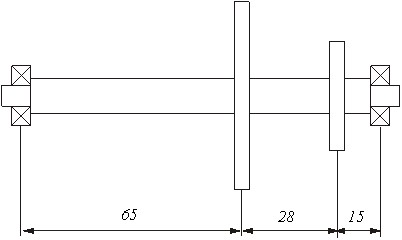
диаметр второго вала определим из технолологического требования, задаваемого отношением б) расчёт вала на прочность и жёсткость Расчетная схема представлена на рис. 3.
Рис. 3. Расчетная схема. В соответствии с условиями работы выбираем для вала сталь 40Х ГОСТ 1050-74 со следующими характеристиками:
Значение крутящего момента на валу T = 3500 Н⋅мм Диаметр вала d под посадку зубчатого колеса (т. к. вал тихоходный принимаем [τ] = 45Мпа):
Диаметр под шарикоподшипники принимаем равным 5 мм , подшипники ГОСТ 8338-57 с характеристиками:
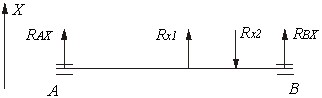
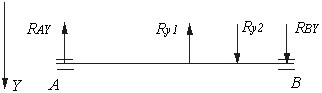
Определим расчетные нагрузки и опорные реакции:
По полученным значениямрасчетных нагрузок определяем опорные реакции в вертикальной и горизонтальной плоскостях. Вертикальная плоскость XOZ:
Для определения нагрузок, действующих на вал в этой плоскости
Горизонтальная плоскость ZOY:
Результирующие нагрузки, действующие на вал со стороны подшипников:
Для определения наиболее опасного сечения построим эпюры изгибающих моментов: в вертикальной плоскости:
в горизонтальной плоскости:
Из построенных эпюр видно, что самым опасным сечением является сечение С. Определим действующие моменты и напряжения в этом сечении. Суммарный изгибающий момент:
Для вала с принятым диаметром равным 8 мм будем иметь:
Напряжение при изгибе
Напряжение при кручении
Номинальное эквивалентное напряжение в опасном сечении:
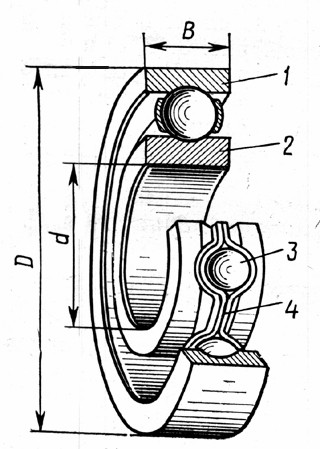
2.4. Расчёт и подбор подшипников Радиальные однорядные шарикоподшипники. [5]Подшипники качения обычно состоят из двух колец — наружного 1 и внутреннего 2, между которыми размещают тела качения 3 (шарики или ролики), отделяемые друг от друга сепараторами. Наружное кольцо служит для крепления подшипника в корпусе, а внутреннее — для крепления на валу.
По сравнению с подшипниками скольжения подшипники качения имеют меньшие моменты трения при трогании с места и в процессе движения, в частности момент трогания, в 5 . . 10 раз меньше, чем у подшипников скольжения; обеспечивают высокую точность центрирования при восприятии значительных радиальных и осевых нагрузок; сохранение работоспособности при больших частотах вращения и в широком диапазоне изменения температуры; стандартизованы и нормализованы в пространстве, что сокращает время проектирования опор вращения, обеспечивает полную взаимозаменяемость, уменьшает стоимость опорных узлов. В опорах приборов, работающих как правило, при малых нагрузках, наибольшее применение получили радиально однорядные и радиально-упорные однорядные шарикоподшипники. [4]Шарикоподшипники радиальные однорядные могут воспринимать не только однорядные, но и осевые нагрузки, действующие в обоих направлениях вдоль оси вала и не превышающие 70 % неиспользованной радиальной нагрузки. Эти подшипники имеют самое широкое применение благодаря своей дешевизне, нетребовательности к точности монтажа и условиям смазки. Их обычно применяют в узлах со сравнительно лёгкими условиями эксплуатации при отсутствии ударных нагрузок и значительно кратковременных перегрузок. Такие подшипники устанавливают, как правило, в качестве опор в лёгких редукторах приборов и приборных устройств, в электродвигателях малой мощности, в коробках передач и других приборных устройствах. Обычно такие подшипники применяют для установки валов с расстоянием между опорами L < 10d (где d — диаметр вала), а также жёстких двухопорных валов, прогиб которых под действием внешних сил не вызывает большого смещения оси вала относительно оси посадочного отверстия. Допустимая величина угла наклона цапфы вала в радиальных шарикоподшипниках θ ≤ 0,01 рад. Соосность посадочных мест на валах под подшипники должна быть выдержана так, чтобы перекос наружних колёс относительно внутренних не превышал 0,004 рад, даже при радиальном увеличенном радиальном зазоре в подшипнике. Шарикоподшипники в опорах приборных устройств могут работать в различных условиях. При малой частоте вращения подшипника n ≤ 1 мин-1 действующие на него внешние нагрузки рассматриваются как статические. Некоторые подшипники качения приборов периодически подвергаются нагрузкам без вращения. При относительно больших статических нагрузках в результате недостаточной контактной прочности на рабочих поверхностях колец подшипников и тел качения могут образовываться вмятины, связанные с местными пластическими деформациями, что является одним из видов разрушения подшипников качения. Для предотвращения указанных пластических деформаций подшипники качения рассчитывают (выбирают) по статической грузоподъёмности. Большинство подшипников приборов работает в динамических условиях при частоте вращения n > 1 мин-1. В этом случае при действии внешних нагрузок перекатывания тел качения по кольцам сопровождается знакопеременными напряжениями в поверхностных слоях контактирующих тел. При недостаточной контактной прочности в результате многократного восприятия знакопеременных напряжений происходит усталостное выкрашивание поверхностей качения шариков м колец в виде образования микротрещин, раковин и отслаивания. Для предотвращения усталостного выкрашивания подшипники качения рассчитывают (выбирают) по динамической грузоподъёмности. При всех условиях работы эксплуатационные характеристики подшипников (долговечность, виброустойчивость, жёсткость, точность и так далее) существенно зависят от распределения нагрузки между телами качения и контактных напряжений в деталях подшипников, что, в свою очередь, определяется расположением оси подшипника и направлением действия нагрузок. Расчет: Выберем подшипник сверхлёгкой серии 1000095, с характеристиками:
где n = 4 об/мин (скорость вращения на данном колесе); V = 1, так как вращается внутреннее колесо подшипника;
X = 1, Y = 0 — коэффициенты радиальной и осевой нагрузок. Следовательно Р определяется по формуле:
Отсюда находим: PА = 1⋅1⋅64⋅1⋅1 = 64 H
Так как табличное значение С = 440 Н, предварительно выбранного подшипника 1000095, превышает расчётное, то есть требуемое 85 Н, то этот подшипник можно установить в данной конструкции.
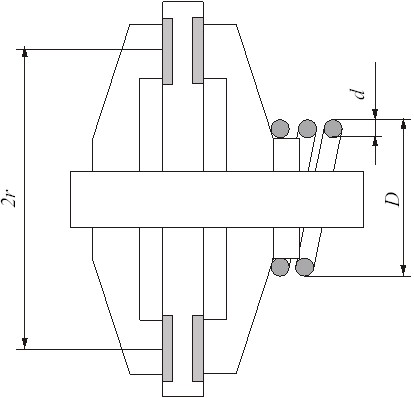
Исходные данные для расчета: r = 28 мм M = 3,5 Н м f = 0.32
Требуется расчитать диаметр проволоки d, количество витков i и зазор между витками. Расчет: Определим силу прижатия N:
Для пружины выбираем материал Ст 45 (проволока) со следующими характеристиками:
Расчеты показывают, что касательное напряжение от перерезывания меньше чем от момента кручения. Поэтому проверочным условием будет:
Отсюда:
С = 7 ... 12 - индекс пружины;
Для значений С = 7 ... 11 расчитаны значения d и D, а результаты занесены в таблицу :
Исходя из конструктивных соображений выбираем проволоку диаметром d = 4,0 мм. Положим число рабочих витков ip = 2, тогда зазор между витками пружины в расслабленном состоянии равен:
Н = λ + iП⋅dВИТКА+0,1⋅iP⋅ dВИТКА = 4,33 + 2,5⋅4,0 + 0,1⋅4,0⋅2 = 21,05 ± 6,3 мм — длина пружины в разжатом состоянии (± 6,3 мм — 30% погрешность) Длина проволоки L: L = πDiп=3,14159⋅40⋅2,5=225 мм. III. Список использованной литературы
Поделитесь этой записью или добавьте в закладки |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||